返回農曆編算法則
農 曆 法 則 之 疑 惑
初稿: 2018年10月 最近一次重大修訂: 2019年4月
看了農曆的編算法則後,也許讀者會感到疑惑:為什麼要這樣編制農曆?
陰陽曆的重點是既要考慮月亮盈虧週期(朔望月),也要照顧季節交替週期(回歸年)。法則三顯然是為了照顧月相。把朔日定為初一,保證初一看不見月亮,農曆月的各日也大致有相同的月相,例如望(滿月)發生在每月的十六日左右。法則四和法則五則是為了使農曆月份不偏離季節。把冬至定在十一月,保證十一月是冬天,因此十一月又稱「冬月」。但是冬至與月相無關,某年的冬至可以發生在朔日,另一年卻可以發生在朔日前一天(又稱「晦日」)。結合法則三,可推斷冬至可以在十一月初一,也可以在十一月最後一日。所以冬至在農曆有三十天的浮動,而在公曆只有三天浮動。
順治二年(1645年)曆法改革前,農曆的月份與中氣有一一對應關係,例如正月必含雨水,二月必含春分等。順治曆改後,這樣的對應關係仍然在大多數時候成立,但會有少數例外,這點在二十四節氣網頁有詳細說明。然而即使在那些少數例外裡,中氣也只是偏離了對應月份僅僅一天而已,因此可以說所有中氣在農曆有約三十天的浮動。所有二十四節氣在公曆裡只有三天浮動,比農曆小得多,這是農曆要兼顧陰陽兩週的代價。
中國在春秋戰國時已發現235(=19×12+7)個朔望月與19個回歸年的時間非常接近,於是採用十九年七閏法編制農曆,即在十九個農曆年裡放置七個閏月。古時稱十九為章歲,七為章閏。後人把章歲和章閏合稱為閏週。
有不少書籍和文章說農曆用十九年七閏法來兼顧陰陽兩週,談到如何在十九年裡加七個閏月時就說以無中氣的月份定為閏月。或許讀者會感到疑惑:以無中氣定閏月為什麼能保證在十九年裡置七個閏月?答案是「不能保證」!首先,「無中氣」置閏法在順治曆改後已廢除,在現行置閏法則下,無中氣的月份雖然大多數確是閏月,但有少數例外。再則十九年七閏法其實在南北朝末期到隋唐間基本上已廢除,原因是19個回歸年比235個朔望月短約二小時,用十九年七閏法制定的曆法(例如猶太曆)在228年會有一日偏差。
戰國至魏晉期間中國的曆法確是採用十九年七閏法,自漢武帝太初元年(公元前104年)起開始採用無中氣法設置閏月。唐朝以前的曆法用平朔法計算合朔,即假設月亮和太陽在天空運行速度是均勻的,兩合朔之間的時間間隔是常數。南北朝以前的曆法一般採用的回歸年與朔望月的比例是235:19,所以19歲正好有235個月。每歲有12個中氣,19歲就有228個中氣,235=228+7,所以有七個月不含中氣,因此以無中氣法置閏能保證十九年有七個閏月。
後來因觀測精度提高,發現十九年七閏法稍嫌粗糙,於是廢棄了回歸年:朔望月=235:19的比例。例如南北朝時期祖沖之創制的《大明曆》實行三百九十一年一百四十四閏,具體做法是取回歸年:朔望月=4836:391,4836 = 391×12 + 144,用無中氣法置閏得391年144閏。這稱之為「破章法」,即打破章閏之法,第一部採用破章法的曆法是《玄始曆》(600年221閏),由北涼國太史著,在北涼行用了28年,在北魏行用了71年。到了唐朝,合朔計算改用定朔,兩合朔的時間間隔不再是常數,到了清朝,連二十四節氣也改用定氣法計算,兩中氣的時間間隔也不再是常數,無中氣法也要修改成現行的置閏法,這樣更不能保證十九年有七個閏月。
雖然閏週只是近似週期,細看按現時置閏法則的閏月分佈,不難發現閏月規律大致符合十九年週期。下表列出從農曆N1930到N2500幾百年間的閏月,分三十行每行七欄排列,每行代表一個閏週的閏月。如前述,法則一在1929年才實施,所以表列的年份從1930年起,以確保所列的閏月都是按相同法則而定。
| 閏週 | 農曆年: 閏月 | ||||||
|---|---|---|---|---|---|---|---|
| 1 | N1930: 六 | N1933: 五 | N1936: 三 | N1938: 七 | N1941: 六 | N1944: 四 | N1947: 二 |
| 2 | N1949: 七 | N1952: 五 | N1955: 三 | N1957: 八 | N1960: 六 | N1963: 四 | N1966: 三 |
| 3 | N1968: 七 | N1971: 五 | N1974: 四 | N1976: 八 | N1979: 六 | N1982: 四 | N1984: 十 |
| 4 | N1987: 六 | N1990: 五 | N1993: 三 | N1995: 八 | N1998: 五 | N2001: 四 | N2004: 二 |
| 5 | N2006: 七 | N2009: 五 | N2012: 四 | N2014: 九 | N2017: 六 | N2020: 四 | N2023: 二 |
| 6 | N2025: 六 | N2028: 五 | N2031: 三 | N2033: 十一 | N2036: 六 | N2039: 五 | N2042: 二 |
| 7 | N2044: 七 | N2047: 五 | N2050: 三 | N2052: 八 | N2055: 六 | N2058: 四 | N2061: 三 |
| 8 | N2063: 七 | N2066: 五 | N2069: 四 | N2071: 八 | N2074: 六 | N2077: 四 | N2080: 三 |
| 9 | N2082: 七 | N2085: 五 | N2088: 四 | N2090: 八 | N2093: 六 | N2096: 四 | N2099: 二 |
| 10 | N2101: 七 | N2104: 五 | N2107: 四 | N2109: 九 | N2112: 六 | N2115: 四 | N2118: 三 |
| 11 | N2120: 七 | N2123: 五 | N2126: 四 | N2128: 十一 | N2131: 六 | N2134: 五 | N2137: 二 |
| 12 | N2139: 七 | N2142: 五 | N2145: 四 | N2147: 十一 | N2150: 六 | N2153: 五 | N2156: 三 |
| 13 | N2158: 七 | N2161: 六 | N2164: 四 | N2166: 十 | N2169: 六 | N2172: 五 | N2175: 三 |
| 14 | N2177: 七 | N2180: 六 | N2183: 四 | N2186: 二 | N2188: 六 | N2191: 五 | N2194: 三 |
| 15 | N2196: 七 | N2199: 六 | N2202: 四 | N2204: 九 | N2207: 六 | N2210: 四 | N2213: 三 |
| 16 | N2215: 七 | N2218: 五 | N2221: 四 | N2223: 九 | N2226: 七 | N2229: 五 | N2232: 三 |
| 17 | N2234: 八 | N2237: 五 | N2240: 四 | N2242: 十一 | N2245: 六 | N2248: 五 | N2251: 三 |
| 18 | N2253: 七 | N2256: 六 | N2259: 五 | N2262: 正 | N2264: 七 | N2267: 五 | N2270: 三 |
| 19 | N2272: 八 | N2275: 六 | N2278: 四 | N2281: 二 | N2283: 六 | N2286: 五 | N2289: 三 |
| 20 | N2291: 七 | N2294: 六 | N2297: 四 | N2300: 二 | N2302: 六 | N2305: 五 | N2308: 三 |
| 21 | N2310: 七 | N2313: 六 | N2316: 四 | N2318: 十 | N2321: 七 | N2324: 五 | N2327: 三 |
| 22 | N2329: 八 | N2332: 六 | N2335: 四 | N2338: 三 | N2340: 七 | N2343: 五 | N2346: 四 |
| 23 | N2348: 八 | N2351: 六 | N2354: 五 | N2357: 正 | N2359: 七 | N2362: 五 | N2365: 四 |
| 24 | N2367: 八 | N2370: 六 | N2373: 五 | N2376: 二 | N2378: 七 | N2381: 五 | N2384: 四 |
| 25 | N2386: 十 | N2389: 六 | N2392: 四 | N2395: 二 | N2397: 六 | N2400: 五 | N2403: 三 |
| 26 | N2405: 八 | N2408: 六 | N2411: 五 | N2414: 二 | N2416: 七 | N2419: 五 | N2422: 三 |
| 27 | N2424: 八 | N2427: 六 | N2430: 四 | N2433: 三 | N2435: 七 | N2438: 五 | N2441: 四 |
| 28 | N2443: 八 | N2446: 七 | N2449: 五 | N2452: 三 | N2454: 八 | N2457: 五 | N2460: 四 |
| 29 | N2462: 八 | N2465: 六 | N2468: 五 | N2471: 三 | N2473: 七 | N2476: 五 | N2479: 四 |
| 30 | N2481: 十 | N2484: 六 | N2487: 五 | N2490: 三 | N2492: 七 | N2495: 五 | N2498: 四 |
從表中可見閏月確是大致符合十九年週期,例如每一欄的年份確是大多數相差十九年,但有若干例外。粉紅色的方格表示閏月的年份偏離了十九年的規律,例如第三閏週的最後一個閏月早了幾個月出現。每一欄的閏月也大致上閏同一個月,但也有例外。黃色方格表示閏月出現的月份「錯了」,意思是說閏月的月份與其在此欄的其他閏月有頗大偏差。例如在第六閏週裡,N2033的閏月出現在閏十一月,而該欄的其他閏月一般是閏七月、閏八月或閏九月。有趣的是第四欄的閏月在第十七閏週前一般是閏七月、閏八月或閏九月,出見了一連串「錯誤」的閏月後,索性「錯到底」,到了第十七閏週以後改為閏正月、閏二月或閏三月。這些偏離閏週的「異常情況」顯示了閏週只是閏月的近似週期,要使農曆不偏離陰陽兩週,在幾百年內需要有若干閏月打破閏週的規律。
從表中可見自1930年後閏正月會首次出現在N2262,其實這是自順治曆改(1645年)後首次出現的閏正月。
最後要指出目前不能很準確計算幾百年後的朔和二十四節氣的UTC+8時刻,這是因為地球自轉不均勻,以致難以準確預測幾百年後會有多少閏秒加到UTC上。公元2200年後的時間計算或會有幾分鐘誤差,如果朔或節氣時間發生在離午夜零時幾分鐘之內,朔日和節氣日期或會有一日偏差,這一日之差一般不會影響閏月的編排,但在少數的情況下或會改變閏月,所以上表列出的數據可能有一兩個會有錯,但不會影響閏月的整體分佈。
乍看農曆編算的法則,似乎不易從中推出農曆年和農曆月的平均週期。其實要估計農曆年月的平均日數不難:農曆月的平均長度應接近朔望月的平均值29.530589日,而農曆年的平均長度應接近回歸年365.2422日。這估計是用反證法而得。假設農曆月的平均長度與朔望月的平均值有頗大偏差,則朔的平均時刻在農曆月裡會漸漸漂移,最終會漂離初一日,但這與法則三相悖,所以原先的假設不成立。同理,假設農曆年的平均值頗大地偏離回歸年,則冬至的平均時刻在農曆十一月會漸漸漂移,最終會漂離十一月,但這與法則四相悖,所以原先的假設不成立。這樣的論述只是估算而不是嚴格證明,其一是因為平均值的運算沒有準確界定,其二是朔望月平均值和回歸年都隨時間而變。
這裡再展示好一點的計算。用FY+k(k是整數)表示農曆年NY+k正月初一UTC正午的儒略日數(所以FY+k是整數);用WY+k表示在公曆Y+k年冬至時刻的儒略日數(所以WY+k一般不是整數);設定ΔFY+k=FY+k - WY+k-1,是從Y+k-1年的冬至到農曆年NY+k正月初一UTC正午的日數。農曆年從NY到NY+n這n年的平均日數是
Y = (FY+n+1 - FY) / n = (WY+n - WY-1) / n + (ΔFY+n+1 - ΔFY) / n
(WY+n - WY-1) / n 是兩冬至在Y-1到Y+n年間的平均日數,這個平均值接近回歸年。正月初一是在冬至後的第二或第三個朔日,所以|ΔFY+n+1 - ΔFY|必定少於某常數U。已知正月初一在公曆的1月20日和2月20日之間浮動,冬至在公曆12月21日到12月23日左右浮動,所以U應接近30日。U的確實數字不重要,重要的是U是有限的。所以當n增加,|ΔFY+n+1 - ΔFY| / n 就會越來越少,從而推出農曆年的平均日數接近回歸年。用類似的方法可以得出農曆月的平均日數接近朔望月。
現在來看看實際數據。據我的計算,從N1929到N2200這272農曆年間有99340日,所以農曆年在這272年的平均日數是99340/272=365.22日,比回歸年短約半小時。然而農曆年長度年年不同,其日數在353日與385日之間,標準偏差是14.31日。意味著平均值會隨所取平均的年份而有所變化。例如農曆年在N1929到N2199這271年間的平均日數是365.262日,在N1929到N2198這270年間的平均日數是365.1926日,這些變動主要來自(ΔF1930+n - ΔF1929)/n這項隨著n變化而產生的變動,這變化會隨取平均的年數增加而降底至零。下圖顯示農曆年在N1929到NY的平均日數隨著Y由2150到2200的變化。
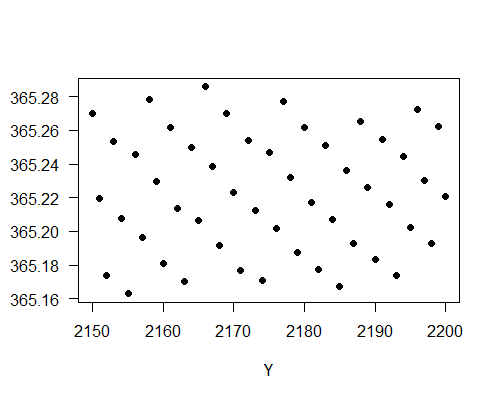
可見農曆年的平均值在365.16日到365.28日之間變動,這就是取270農曆年左右的平均值的結果,要減少平均值的變化,可取更多農曆年的平均值。下圖顯示農曆年在N1929到NY的平均日數隨著Y由2878到2928的變化。取平均值的農曆年數高達一千。
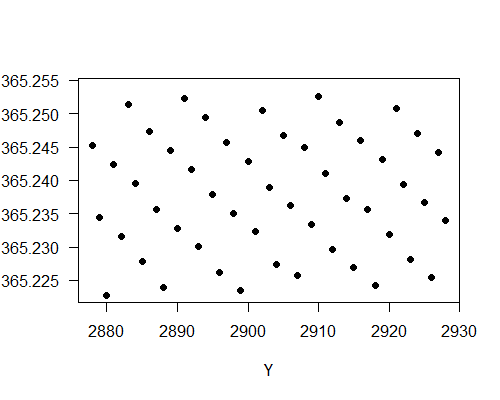
圖中可見農曆年數目增加到一千左右時,其平均日數在365.224日與365.255日之間變動,變化幅度小了約四倍。這正與預期的一致,因為變動幅度應與n成反比,此處n是取平均的年數。農曆年的平均日數確是接近回歸年365.242日。
現在再看農曆月的平均日數,從N1929到N2200這272農曆年間有3364個農曆月(包括閏月),前面說過這272農曆年有99340日,所以農曆月在這3364個月的平均日數是99340/3364=29.5303日。為了知道這個平均值隨月數的變化,下圖顯示農曆月在N1930起算的第一個月到第M個月的平均值隨著M由3300到3364的變化。
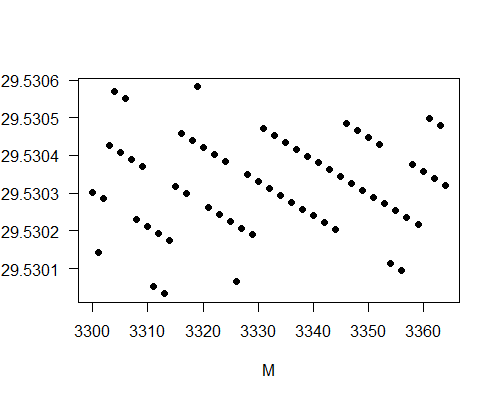
圖中可見農曆月平均值的變化遠少於農曆年的平均值變化,這是由兩個因數造成。其一是農曆每月的日數變化只有一日(二十九日或三十日),其二是現在在取幾千個數的平均值,而不是幾百個數的平均值。農曆月在這三千幾個月的平均日數在29.5300日和29.5306日之間變動,確是接近朔望月的平均值29.530589日。
返回農曆編算法則