Computation of the Ancient Six Calendars
First draft: March, 2019
The information described here is based on Section 3.6 of the book Ancient Chinese Calendars and AlmanacsZCBH08 by Zhāng Péiyú (張培瑜), Chén Měidōng (陳美東), Bó Shùrén (薄樹人), and Hú Tiězhū (胡鐵珠). According to the preface, the chapters in the book were written separately by the four authors. Chapter 3 was written by Zhāng Péiyú, a researcher in the Purple Mountain Observatory in Nanjing, China. I do not use the exact same method to calculate the ancient six calendars described in the book, but use a method that is more convenient for implementation on a computer. The results agree with the calendar data in Zhāng Péiyú's two books Tables of Chinese Calendars in the Pre-Qin PeriodZhang87 and 3500 Years of Calendars and Astronomical PhenomenaZhang97.
Contents
- The Sìfēn System
- Epochs
- Computation of Lunar Conjunctions and Solar Terms
- Order of Months
- Intercalation Rules
- Examples of Computing the Ancient Six Calendars
- Using Decimals to Compute the Ancient Six Calendars
In the Warring States period (480 BCE – 221 BCE), China was divided into many states. Each state used its own calendar. It was believed that there were six versions of calendars used by the states at that time. They are collectively called gǔliùlì (古六曆) or ancient six calendars. These six calendars were Zhou, Lu, Huangdi, Yin, Xia and Zhuanxu. They were all based on the sìfēn system. In Chinese, the term sìfēn (四分) means "division by four" or "quarter." It comes from the fact that the sìfēn system uses 365.25 days as the solar cycle (tropical year), i.e. 365 and a quarter days. The sìfēn system adopts a lunar cycle (synodic month) that is 19/235 of its solar cycle. That is,
lunar cycle = (365 + 1/4) days × 19/235 = (29 + 499/940) days. As a result, 235 lunar cycles are exactly equal to 19 solar cycles. Since 235=19×12+7, if there are 12 lunar months in each year, there will be 7 extra months in 19 years. So 7 intercalary or leap months are added to the calendar every 19 years to keep the calendar year in sync with the solar cycle. This is the basis of the sìfēn system. The 19-year cycle was called the zhāng cycle (章週) in China. It was known as the Metonic cycle (named after the Greek astronomer Meton of Athens) in the West. Hereafter, the terms lunar cycle and solar cycle will be referred to as the values adopted by the sìfēn system.
The ancient six calendars were all based on the sìfēn system. They differ by their choices of liyuan (曆元) or epochs. Here the term epoch is used to refer to an instant in time chosen as a reference point from which time is measured. It was usually chosen so that a particular solar term (usually the winter solstice) was assumed to occur at the same time as the lunar conjunction (and usually at midnight).fn1
Take the Zhou calendar as an example. Its epoch is chosen when the winter solstice and conjunction was assumed to occur at midnight on a particular day with the sexagenary cycle of jiǎ zǐ. Before the 7th century CE, calculation of the conjunction time was based on the píngshuò (平朔) method and calculation of time of the solar terms was based on the pínqì (平氣) method. These methods assume that the motions of the Sun and Moon in the sky are uniform (mean motions). By definition, the conjunction and winter solstice both occurred at midnight at the epoch of the Zhou calendar. Since one solar cycle = (12 + 7/19) lunar cycles, the winter solstice in the following year would be 7/19 lunar cycles after the conjunction. Thus the winter solstice and conjunction were no longer at the same time. The number 7/19 is called rùnyú (閏餘) or intercalation remainder.
In general, rùnyú is defined as the age of the Moon at a particular solar term (usually the winter solstice), which is the time of the solar term measured from its previous lunar conjunction time. It can be expressed in days or as a fraction of the lunar cycle. For simplicity, I use "lunation fraction" to refer to the age of the Moon expressed as a fraction of a lunar cycle. Thus rùnyú began with 0 at the epoch, and became 7/19 one year later. It is easy to show that the lunation fraction of any solar term increases by 7/19 every year. When it reaches or exceeds 1, it will need to be subtracted by 1. Using this rule, we can easily figure out the first 19 rùnyús in the Zhou calendar starting from the epoch: 0, 7/19, 14/19, 2/19, 9/19, 16/19, 4/19, 11/19, 18/19, 6/19, 13/19, 1/19, 8/19, 15/19, 3/19, 10/19, 17/19, 5/19, and 12/19. In the 20th year the rùnyú returns to 0 and the cycle repeats. Thus rùnyú has a cycle of 19 years, the zhāng cycle.
Since 365.25×19=6939.75, after one zhāng cycle even though the winter solstice and conjunction occur at the same time again, the time is not at midnight but at 18 o'clock. It takes four zhāng cycles for the winter solstice and conjunction to both occur at midpoint again. Four zhāng cycles is called a bù (蔀) cycle, which is 76 years. One bù cycle has 365.25×76 days = 27759 days, which is not a multiple of 60 days. Even though the winter solstice and conjunction both occur at midnight again after one bù cycle, the sexagenary day is not jiǎ zǐ as at the epoch. It takes 20 bù cycles for the sexagenary cycle to return to the same as at the epoch. Twenty bù cycles is called a jì (紀) cycle, which is 1520 years. 1520 is not a multiple of 60, so even though the winter solstice and conjunction both occur at midnight on a jiǎ zǐ day, the sexagenary cycle of the year is not the same as that at the epoch. It takes 3 jì cycles for the sexagenary year to return to the same sexagenary year as the epoch. Three jì cycles is called a yuán (元) cycle, which has 4560 years. The following summarizes the cycles in the sìfēn system.
Lunar cycle: 1 lunar month = (29 + 499/940) days
Solar cycle: 1 solar year = (365 + 1/4) days = (12 + 7/19) lunar months
Zhāng cycle: 19 (solar) years = 235 (lunar) months = 6939.75 days
Bù cycle: 4 zhāng cycles = 76 years = 940 months = 27759 days
Jì cycle: 20 bù cycles = 1520 years = 18800 months = 555180 days
Yuán cycle: 3 jì cycles = 4560 years = 56400 months = 1665540 days
The ancient six calendars were developed and used in the Warring States period, but none of them was preserved. We can now only learn about them in books such as Hànshū (漢書 or Book of Han) published in the first century CE, and Xù Hànshū (續漢書 or Sequel of the Book of Han) published in the third century CE. The two books do not provide concrete information about the epochs used by the six calendars. The earliest available information on the epochs is found in the book Kāiyuán Zhánjīng (開元占經 or Divination Classic Complied in the Kāiyuán Era) published in the 8th century. The epochs are listed as the number of years between 714 CE and shàngyuáns (上元), which I will refer to as superior epochs hereafter. A superior epoch was considered to be an ideal epoch at which the Sun and Moon had the same longitude and the five planets were in the same direction in the sky. "Same direction" was a vague description, which was made precise by Chinese astronomers in the Qing dynasty (1644–1911) to mean the angular separations among the five planets were less than 45°. The following table lists the superior epochs of the six calendars. Shàngyuán jīnián (上元積年) refers to the number of years between 714 CE and the superior epoch.
| Calendar | Shàngyuán Jīnián | Superior epoch in proleptic Julian Calendar | Relationship between solar term and conjunction at the epoch |
|---|---|---|---|
| Huangdi | 2760863 | -2760149 | Winter solstice and conjunction occurred at midnight on a jiǎ zǐ day |
| Yin | 2761080 | -2760336 | |
| Zhou | 2761137 | -2760423 | |
| Xia | 2760589 | -2759875 | Xia calendar has two versions. Version 1 specifies winter solstice and conjunction occurring at midnight on a jiǎ zǐ day. Version 2 specifies Z1 and conjunction occurring at midnight on a jiǎ zǐ day. |
| Zhuanxu | 2761019 | -2760305 | J1 and conjunction occurred at midnight on a jǐ sì day. |
| Lu | 2761514* | -2760800 | Winter solstice occurred at midnight on a jiǎ zǐ day with a rùnyú of 1/19 |
* Many scholars pointed out that the number listed in Kāiyuán Zhánjīng is wrong. The number listed here is based on the calculation by Zhāng Péiyú.
In the table, solar terms other than winter solstice are indicated by the labels used on our solar terms page. J1 (立春 or Beginning of Spring) is the third solar terms following the winter solstice; Z1 (雨水 or Rain Water) is the fourth solar terms following the winter solstice. As indicated in the table, the Xia calendar has two versions. Version 1 specifies the winter solstice and conjunction occurring at midnight on a jiǎ zǐ day. Version 2 specifies the solar term Z1 and conjunction occurring at midnight on a jiǎ zǐ day. Hereafter, I will call the first version as the "solstice version" and the second version as the "Z1 version."
The case of the Lu calendar needs further explanation. First, many scholars pointed out that the number for the superior epoch in Kāiyuán Zhánjīng was wrong. The values listed in the table are based on the calculation by Zhāng Péiyú. Second, the Book of Han states that the Lu calendar was "askew" in the sense that the rùnyú was 1/19 in the beginning year of its bù cycle. That is to say that at the Lu epoch listed in the table above, the winter solstice occurred at midnight on a jiǎ zǐ day, but the conjunction occurred 1/19 lunar cycles (=1.554 days) earlier. Strictly speaking, the Lu epoch does not qualify as a superior epoch because of the misalignment of the Sun and Moon. The superior epochs of all the other calendars specify a particular solar term and conjunction occurring at the same time, which means that the rùnyú is 0 at the epoch.
The concept of superior epoch was introduced by Liú Xīn (劉歆) in the first century BCE. The computation of superior epoch is a tedious exercise in modular arithmetic. Since the simultaneous alignment of the Sun, Moon and five planets is very rare, the superior epoch was in the remote past very far away from the time the astronomical system was developed. Here I use the term astronomical system instead of calendar for the Chinese term lì (曆) because lì was actually a system of mathematical astronomy developed to calculate the motions of the Sun, Moon and planets. Calendar calculation was just one function of lì. As the measurement accuracy improved over time, it was apparent that the periods of the Sun, Moon and planets were not commensurate with each other. They had to be approximated by more and more complicated fractions and the superior epoch moved further and further into the remote past. For example, the Chúnyòu astronomical system (淳祐曆) developed in 1250 placed the superior epoch in the year 120,266,428 BCE! The large number made the astronomical calculations inconvenient. A more serious problem was that as the astronomical system became more and more complciated (e.g. by including more constants for describing the non-uniform motion of the Sun and Moon), the calculation of superior epoch became too tedious that the algorithm had to be simplified. Astronomical constants were first determined by observations, but were modified in order to match the superior epoch determined by the simplified algorithm. The superior epoch system was abadoned in 1280s and astronomical constants were determined entirely from observations. Further information on the superior epoch and its calculation can be found here.
The superior epochs listed in Kāiyuán Zhánjīng are most likely calculated by people in the later Han dynasty (25 – 220 CE), not the epochs used in the Warring States period. It is more convenient to use epochs closer to the Warring States period than the ones listed in Kāiyuán Zhánjīng. From the previous Section, we know that after a jì cycle (1520 years), the times of conjunction, solar terms and the sexagenary day return to the same values. We can therefore add integer multiples of 1520 years to the epochs in Kāiyuán Zhánjīng to find other more convenient epochs. Take the Zhou calendar as an example. its superior epoch is in the year -2760423. Adding 1520×1816=2760320 to the number yields -103, or 104 BCE. That is to say that we can take the midnight on a jiǎ zǐ day in 104 BCE. as an epoch for the Zhou calendar. At this epoch, the winter solstice and conjunction were assumed to occur at midnight on a jiǎ zǐ day. Note that the Chinese calendar is a luni-solar calendar. The months are arranged according to the Moon's phases, and the years are arranged according to the Sun's position. The winter solstice is often considered as the beginning of a "solar year," or suì (歲). Thus, the winter solstice of 104 BCE actually refers to the winter solstice that is closest to Jan. 1, 104 BCE, which fell in late December in 105 BCE. The Zhou calendar's epoch in "104 BCE" can be easily determined by finding the jiǎ zǐ day in late December in 105 BCE, which turns out to be on 25 December, 105 BCE.
We don't need to use a jiǎ zǐ day as an epoch. Adding an integer multiples of the bù cycles will yield an epoch at which a solar term and conjunction having the same relationship as at the superior epoch. Take the Zhou calendar as an example, subtracting 76×3 years from -103 yields -331. That is to say that the winter solstice and conjunction also occurred at midnight in 332 BCE (actually late December in 333 BCE). Now 76×3 years = 228 years = 83277 days. Straightforward calculation shows that 83277 days before December 25, 105 BCE was December 25, 333 BCE. The sexagenary day can be calculated, using modular arithmetic, to be dīng mǎo. A bù cycle can be named after the sexagenary name of its first day in the cycle. Thus, 104 BCE was the first year in the bù cycle of jiǎ zǐ of the Zhou calendar. The year 332 BCE was the first year in the bù cycle of dīng mǎo, 331 BCE was the second year in the bù cycle of dīng mǎo and so on.
The epochs of the ancient six calendars are different, which means that the six calendars have six different origins from which time is measured. This is inconvenient for developing a general procedure to compute the calendars. Here I introduce a method to simplify the calculation.
This method uses Julian days to represent times. The Julian day is defined as the number of days counted from January 1, 4713 BCE at noon. Using Julian days is a way to ignore the epochs of the six calendars and unify the time origin to be at noon on January 1, 4713 BCE. Take the Zhou calendar as an example, I find from the previous section that the midnight of December 25, 105 BCE was an epoch at which conjunction and winter solstice were assumed to occur. The Julian day was 1683430.5. Using the píngshuò and pínqì rules, the Julian days of the conjunctions and winter solstices in the Zhou calendar can be written as
JD(Mi) = 1683430.5 + i·PL
JD(W(y)) = 1683430.5 +(y+103)·Ps
Here PL=(29+499/940) is the lunar cycle, Ps=365.25 is the solar cycle, Mi is the ith conjunctions after the conjunction at midnight of December 25, 105 BCE W(y) is the winter solstice closest to Jan. 1 in year y, which fell in late December in year y-1. In general, the Julian days of the conjunctions and winter solstices in all six calendars can be written in the form
JD(Mi) = JD(M0) + i·PL (1)
JD(W(y)) = JD(W(y0)) + (y-y0)·Ps (2)
Here i refers to the lunation number from the conjunction M0 at the epoch. The values of JD(M0), JD(W(y0)) and y0 are constants for each of the six calendars and are given in Table 2 below. It is convenient to combine JD(W(y0)) and y0 into a new variable JDw:
JDW=JD(W(y0)) - y0·Ps (3)
The Julian days of the winter solstices are simplified to
JD(W(y)) = JDW + y·Ps (4)
The values of JDW are listed in the last column of Table 2.
| Calendar | JD(M0) | JD(W(y0)) | y0 | JDW |
|---|---|---|---|---|
| Huangdi | 1783510.5 | 1783510.5 | 171 | 1721052.5 + 1/4 |
| Yin | 1704250.5 | 1704250.5 | -46 | 1721051.5 + 1/2 |
| Zhou | 1683430.5 | 1683430.5 | -103 | 1721050.5 + 3/4 |
| Xia (solstice version) | 1883590.5 | 1883590.5 | 445 | 1721053.5 + 3/4 |
| Xia (Z1 version) | 1883650.5 | 1883589.5 + 1/8 | 445 | 1721052.5 + 7/8 |
| Zhuanxu | 1726575.5 | 1726529.5 + 11/32 | 15 | 1721050.5 + 19/32 |
| Lu | 1545728.5 + 419/940 | 1545730.5 | -480 | 1721050.5 |
The parameter y0 for each calendar is determined by adding an appropriate integer multiples of 1520 years to the superior epoch to bring the year closer to the Warring States period. Since the approximate dates of the solar terms are known (winter solstice: late December, J1: early February, Z1: late February), it is easy to find the dates of the specified sexagenary days in the (proleptic) Julian calendar, which are then used to compute JD(W(y0)) and JD(M0).
Huangdi calendar, Yin calendar, Zhou calendar, and the solstice version of the Xia calendar assume conjunction and winter solstice occurring at the same time at the epochs, so JD(W(y0)) = JD(M0) for these calendars. The Z1 version of the Xia calendar assumes Z1 and conjunction occurring at the same time. Z1 is the fourth solar term after the winter solstice. It follows from the pínqì rule that the winter solstice is (4/24)Ps=60.875 days before Z1. Hence, JD(W(y0)) = JD(M0) - 60.875 for the Z1 version of the Xia calendar. Zhuanxu calendar assumes that J1 and conjunction occurring at the same time. J1 is the third solar term after the winter solstice. Hence the winter solstice is (3/24)Ps=(45 + 21/32) days before J1. Thus, JD(W(y0)) = JD(M0) - (45 + 21/32) for the Zhuanxu calendar. For the Lu calendar, the conjunction occurred (1/19)PL before the winter solstice at the epoch. As a result, JD(M0) = JD(W(y0)) - (1/19)×(29 + 499/940).
Although we don't know if all of the 24 solar terms were invented in the Warring States period, we can still calculate them using the pínqì rule:
JDq(j,y) = JD(W(y)) + (j/24)·Ps (5)
Here j is the solar-term number counting from the winter solstice, with j=0 for the winter solstice (Z11), j=1 for J12, j=2 for Z12, j=3 for J1, ..., j=23 for J11 (see our solar terms page for the order of the 24 solar terms). With the exception of the winter solstice being in late December in year y-1, all other 23 solar terms computed using equation (5) are in year y.
The advantage of using Julian days is that there are standard algorithms for converting Julian days to dates in the Julian/Gregorian calendar. Our sexagenary cycle page also lists formulae for converting Julian days to sexagenary days.
Equations (1), (4) and (5) also give us a new perspective on the structure of the ancient six calendars. The six calendars use píngshuò and pínqì rules to compute conjunctions and solar terms, which is why the Julian days of lunar conjunctions are expressed as a constant plus integer multiples of PL and the Julian days of solar terms are expressed as a constant plus integer multiples of Ps/24. All six calendars are based on the sìfēn system and so they all use the same values of Ps and PL. The six calendars differ from their choices of the two parameters JD(M0) and JDw. Of course, this is equivalent to saying that the six calendars adopt different epochs and different relationships between a solar term and conjunction at the epochs.
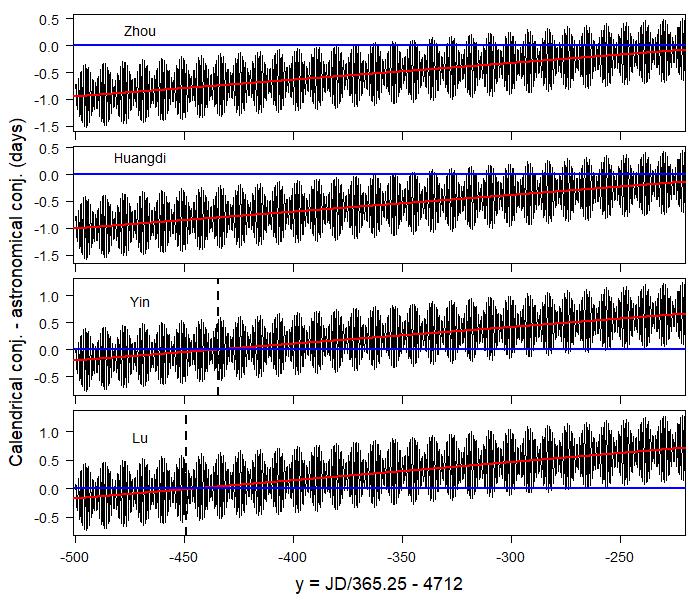
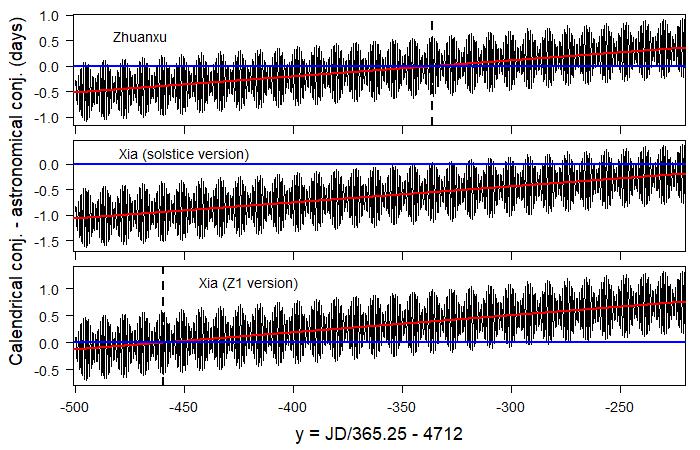
The solar cycle 365.25 of the sìfēn system is exactly the same as the one adopted by the Julian calendar. The solar cycle is 0.0078 days longer than the true tropical year, resulting in a drift of one day every 128 years. The lunar cycle (29 + 499/940) days of the sìfēn system is longer than the synodic month by 0.000268 days, resulting in a drift of one day in 3730 lunar cycles (about 300 years). The different values of the two parameters used by the six calendars not only may arise from the differences in measurements, but also may arise from the fact that these calendars were developed in different times. The figure below shows the time difference between the calendrical and astronomical conjunctions as a function of years for the six calendars. The oscillations are caused by the fact that calendrical conjunctions are calculated by the píngshuò method, which only takes into account the mean motions of the Moon and Sun. As expected, we see that the calendrical conjunctions of all six calendars drift at a steady rate. The mean time difference at a particular time can be calculated by taking an average over several oscillations around that time, or more conveniently by fitting the data using a linear regression since we know the increase is linear in time. The regression lines are shown in red in the figure below. The figure shows that the calendrical conjunctions mostly occurred earlier than the astronomical conjunctions for the Zhou, Huangdi, and the solstice version of the Xia calendars, although the time differences gradually decreased near the end of the Warring States period (222 BCE). The calendrical conjunctions matched most closely to the astronomical conjunctions around 460 BCE for the Z1 version of the Xia calendar, around 450 BCE for the Lu calendar, around 435 BCE for the Yin calendar, and around 335 BCE for the Zhuanxu calendar.
The Zhou, Lu and Huangdi calendars designate the zǐ month (present-day month 11), i.e. the month that the winter solstice is in, as the beginning of a year. The Yin calendar designates the chǒu month (present-day month 12) as the beginning of a yearfn3. Both versions of the Xia calendar adopt the yín month (present-day month 1) as the beginning of a year. Months in these calendars are labelled by numerical numbers from 1 to 12 starting from the first month. The naming of leap months will be discussed later. Zhuanxu calendar is special. The first month is the hài month (present-day month 10) but it is labelled as month 10, the same as the numbering in the Xia calendar. The month orders (excluding leap months) in Zhuanxu calendar are months 10, 11, 12, 1, 2, ..., 9.
Scholars have not come to a consensus on how and where an intercalary (leap) month was placed in the ancient six calendars. Some people think that a leap month was always placed at the end of a year and was simply labelled as a leap month. Others disagree and think a leap month could occur in the middle of a year. A leap month in the middle of a year is indicated by the same number as the previous month, but a "leap" is added before the number. The case for the Zhuanxu calendar is less controversial. It is generally believed that a leap month in the Zhuanxu calendar was placed at the end of a year and was called post month 9 (後九月), but its intercalation rule remains unclear.
Three rules have been proposed as possible intercalation rules. Here I call these three rules the rùnyú rule (閏餘法), solstice rule (固定冬至法) and no zhōngqì rule (無中氣法). The no zhōngqì rule assigns a month that does not contain a major solar term (see below) as a leap month. The solstice rule places a leap month at the end of a year. The rùnyú rule does not specify explicitly where a leap month should be placed. It can be placed at the end of a year or in the middle of a year using a simple rule. The six calendars computed on our calendar page and conversion table page follow the same approach as in Zhāng Péiyú's two books Tables of Chinese Calendars in the Pre-Qin PeriodZhang87 and 3500 Years of Calendars and Astronomical PhenomenaZhang97, which use the solstice rule and place a leap month at the end of a year but also indicate the months without a major solar term for reference.
Let's start with the case for the Zhou calendar and Huangdi calendar. Both of them specify the zǐ month as the beginning of a year.
Recall that a solar cycle = (12 + 7/19) lunar cycles. As mentioned above, rùnyú increases by 7/19 (modulo 1) every year. Both the Zhou calendar and Huangdi calendar assume the winter solstice and conjunction occurring at the same time in the beginning of their bù cycles, which means the winter solstice is on the New Year day and the rùnyú is 0. The winter solstice in the second year is 12 and 7/19 months later and the rùnyú is 7/19. If there is no leap month, it will occur on the 12th day of the first month. In the third year, the rùnyú becomes 14/19. If there is no leap month, the winter solstice will be on the 23rd day of the first month. Since 14/19 + 7/19 exceeds one, the winter solstice in the fourth year is 13 and 2/19 months away from the New Year day of the third year. If there is still no leap month, the winter solstice will occur in the second month. This means that the second month is a zǐ month, which is not acceptable. Therefore, there must be a leap month in the third year in order to make the first month in the fourth year to be a zǐ month. The rùnyú in the fourth month is 2/19. It is easy to see that whenever the rùnyú in a given year reaches 12/19 or larger, an addition of 7/19 will exceed one and there needs to be a leap month in order to keep the first month of the following year to be a zǐ month. Here is the rùnyú rule: a leap month occurs in the year in which the lunation fraction of the winter solstice is equal to or greater than 12/19. We have listed the rùnyús in the Zhou calendar in the first 19 years of the bù cycle in Section 1. The rùnyús of the Huangdi calendar are exactly the same. From the list we see that a leap month occurs in the 3rd, 6th, 9th, 11th, 14th, 17th and 19th years. In the 20th year, the rùnyú returns to 0. Hence the cycle of leap months is 19 years, which is the zhāng cycle. The leap years have the 3-3-3-2-3-3-2 pattern, meaning that a leap month occurs in the 3rd year, (3+3)th year, (3+3+3)th year, (3+3+3+2)th year and so on.
The Lu calendar also designates the zǐ month as the beginning of a year, but the rùnyú is 1/19 in the first year of its bù cycle. From the rùnyús listed in Section 1, we see that this is equivalent to setting the beginning year of the bù cycle in the 11th year of the zhāng cycle of the Zhou and Huangdi calendar. So the leap months occur in the 3rd, 6th, 8th, 11th, 14th, 17th and 19th years when counting from the bù cycle of the Lu calendar.
The other three calendars do not designate the zǐ month as the beginning of their years, but the rùnyú rule can be modified as: a leap month is added to the suì in which the lunation fraction of the winter solstice is equal to or greater than 12/19. Here suì (歲) refers to the period starting on the first day of the zǐ month and ending on the day before the first day of the following zǐ month. Suì and calendar year are the same for the Zhou, Huangdi and Lu calendar. This rule will make the winter solstice always occurring in the 12th month for the Yin calendar, and in the 11th month for the solstice version of the Xia calendar. However, we can only say that the rule will make the winter solstice often occurring in the 11th month for the Z1 version of the Xia calendar and Zhuanxu calendar.
For both the Yin and solstice version of the Xia calendar, the lunation fraction of the winter solstice is 0 in the first suì of the bù cycle. As a result, the suìs containing a leap month are exactly the same as the Zhou and Huangdi calendar. For the Z1 version of the Xia calendar, the lunation fraction of Z1 is 0 in the first suì of its bù cycle. Winter solstice is (1/6) solar cycles before Z1. Since Ps/6 = (2 + 7/114) PL, it is easy to deduce that the lunation fraction of the winter solstice is 107/114 in the first suì of the bù cycle. The lunation fractions in the next 18 suìs can be calculated by adding 7/19 (modulo 1) in each suì. The result is (omitting the denominator 114) 35, 77, 5, 47, 89, 17, 59, 101, 29, 71, 113, 41, 83, 11, 53, 95, 23, and 65. The leap months occur in the 1st, 3rd, 6th, 9th, 12th, 14th and 17th suìs. For the Zhuanxu calendar, the lunation fraction of J1 is 0 in the first suì of its bù cycle. The winter solstice is (1/8)Ps=(1 + 83/152)PL before J1. Hence the lunation fraction of the winter solstice is 69/152 in the first suì of the bù cycle. The lunation fractions in the next 18 suìs are (omitting the denominator 152) 125, 29, 85, 141, 45, 101, 5, 61, 117, 21, 77, 133, 37, 93, 149, 53, 109 and 13. The leap months occur in the 2nd, 5th, 7th, 10th, 13th, 16th and 18th suìs.
The rùnyú rule discussed so far does not specify where a leap month should be placed. It can be placed at the end of a calendar year. However, there is an extension of the rùnyú rule that allows a leap month to be placed in a specific month in the middle of a year. Recall that a leap month occurs in the suì in which the lunation fraction of the winter solstice is equal to or greater than 12/19. Let K be the lunation fraction of the winter solstice, which is ≥ 12/19 when there is a leap month. The lunation fraction of the winter solstice in the following suì increases by 7/19 (mod 1). Dividing the number 7/19 by 12 gives 7/228. Suppose we keep adding 7/228 to K for each of the 12 months after the zǐ month, there must be a month in which the accumulated number will reach or exceed 1. This month is designated as the leap month.
The suìs containing the leap months in the Lu calendar, Z1 version of the Xia calendar and Zhuanxu calendar are different from the other calendars, but they can be made the same by choosing another suì in their bù cycles as the first suì in a zhāng cycle. The leap month distribution in all six calendars follows the 3-3-3-2-3-3-2 pattern. The lunation fractions of the winter solstice have a cycle of 19 years and so do the leap months. It is of course a result of the fact that 19 solar cycles are exactly equal to 235 lunar cycles in the sìfēn system. Since 235=19×12+7, 7 leap months have to be inserted in 19 years. One of the simplest arrangements is to distribute them evenly in these 235 months. One way to do this is to assign the leap months to occur in the (235j/7)th months (j=1, 2, 3, 4, 5, 6, 7) in a zhāng cycle. Taking the nearest integers will result in the leap months occurring in the 34th, 67th, 101st, 134th, 168th, 201st and 235th months. They occur in the 3rd, 6th, 9th, 11th, 14th, 17th and 19th suìs in the zhāng cycle. Here we see the 3-3-3-2-3-3-2 pattern. The Zhou, Yin, Huangdi and solstice version of the Xia calendar all have the lunation fractions of the winter solstice being 0 in the first year of their zhāng cycles. Using the extended rùnyú rule for placing a leap month in the middle of a year, we find the leap months occurring in the 34th, 68th, 101st, 135th, 168th, 202nd and 235th months. These are almost the same as the rounded numbers of (235j/7). The discrepancies are caused by the extended rùnyú rule requiring the accumulated lunation fraction to reach or exceed 1. We get perfect agreement by rounding up the numbers (235j/7). The leap months occur in different months for the Lu calendar, Z1 version of the Xia calendar and Zhuanxu calendar. This is simply caused by their using different months as the first month in their zhāng cycles.
The solstice rule requires that a particular month must contain the winter solstice. The Zhou, Lu and Huangdi calendars designate the zǐ month as the first month of a year. For this reason, the first month must contain the winter solstice. Yin calendar designates the chǒu month as the first month. Chǒu month is one month before the zǐ month, so the solstice rule requires that month 12 must contain the winter solstice in the Yin calendar. The two versions of the Xia calendar assign the yín month as the first month. Yin month is two months after the zǐ month, so the solstice rule requires that month 11 must contain the winter solstice in the two versions of the Xia calendar. Finally, Zhuanxu calendar uses the hài month as the first month but labels it as month 10. The solstice rule requires that month 11 must contain the winter solstice in the Zhuanxu calendar.
As mentioned in the previous subsection, a suì refers to the period starting on the first day of the zǐ month and ending on the day before the first day of the following zǐ month. A suì can contain 12 or 13 months. I call the suì containing 12 months as a "normal suì," and the suì containing 13 months as a "leap suì." Since the solstice rule assigns the zǐ month, the month that contains the winter solstice, to a particular month, there cannot be any leap month in a normal suì and one leap month in a leap suì. The implicitly rule is that all 12 normal months must appear exactly once in any given suì. A leap month is placed in the end of a calendar year.
In many cases the solstice rule and the rùnyú rule agree on which suì a leap month should occur. This is not difficult to understand. Suppose the lunation fraction of the winter solstice is K in a given suì. The conjunction associated with the zǐ month is K lunar cycles before the winter solstice. Since one solar cycle = (12 + 7/19) lunar cycles, the winter solstice in the following suì is (12 + 7/19) lunar cycles after the current winter solstice, which is (12 + K + 7/19) lunar cycles from the conjunction associated with the zǐ month of the current suì. If K<12/19, the second zǐ month is usually 12 months after the first zǐ month and we have a normal suì. If K≥12/19, the second zǐ months is usually 13 months after the first zǐ months and we have a leap suì. Hence, there is usually a leap month if K≥12/19. This is almost the same as the rùnyú rule. It's the "usually" assertion that makes the two rules slightly different. Let's take the Zhuanxu calendar as an example to demonstrate why the two rules can give different results in some cases.
From the rùnyús listed in the previous subsection, we see that the rùnyú in the 15th suì in the bù cycle of the Zhuanxu calendar is 93/152 < 12/19. The rùnyú in the 16th suì is 149/152 > 12/19. According to the rùnyú rule, there is no leap month in the 15th suì but a leap month in the 16th suì. It follows that in the 16th suì the winter solstice is 149/152 lunar cycles from month 11. This means that the conjunction associated with month 12 occurs 3/152 lunar cycles after the winter solstice. Now 3/152 lunar cycles is 13 hours 59 minutes and 18 seconds. If the winter solstice in the 16th suì occurs earlier than 10:00:42, the conjunction associated with month 12 will occur on the same day as the winter solstice. Calculation shows that the winter solstice in the 16th suì occurs at 2:15 and conjunction occurs at 16:13:18 on the same day. That is to say that the winter solstice in the 16th suì falls on the first day of month 12 according to the rùnyú rule, which violates the solstice rule. In China midnight is always considered as the beginning of a day. Even though the winter solstice occurs earlier than the conjunction, they are still regarded as falling on the same day. The solstice rule requires that month 11 must contain the winter solstice. Hence the conjunction that occurs about 14 hours later than the winter solstice is associated with month 11. It then follows that the 15th suì is a leap suì and must have a leap month. The 16th suì does not have a leap month. This shows that the solstice rule sometimes gives a different result from the rùnyú rule.
From the above example, we see that the two rules can give different results when the lunation fraction of the winter solstice is very close to 1 so that it might fall on the same day as the next conjunction. For the Zhou, Lu, Huangdi and solstice version of the Xia calendars, the lunation fractions of the winter solstice are integer multiples of 1/19. This means that the time difference between the winter solstice and the conjunction after it is greater than 1.55 days. It is therefore impossible to have the winter solstice and the next conjunction occurring on the same day. The rùnyú rule and solstice rule give exactly the same result for these calendars.
The no zhōngqì rule also assigns the winter solstice to a designated month in the same way as the solstice rule. Thus a leap month is inserted in a leap suì. The only difference is where a leap month should be placed in a leap suì. The no zhōngqì rule specifies that a leap month is placed in the month that does not contain a major solar term.
As mentioned in the solar terms page, major solar terms refer to the 12 solar terms Z1, Z2, ..., Z12. Under the pínqì rule, the time difference between any two successive major solar terms is Ps/12 = (30+7/16) days, which is longer than 30 days. This means that a month can only contain at most one major solar term. There are always 12 major solar terms in a suì. It follows that each of the 12 months in a normal suì contains a major solar term. In a leap suì, there are 13 months and so exactly one month must not contain a major solar term. The no zhōngqì rule assigns that month without a major solar term in a leap suì as the leap month. Since the zǐ month is assigned to a particular month and a leap month does not contain any major solar term, every major solar term is fixed to be in a particular calendar month. Take the Xia calendar as an example. Month 11 is assigned to be the month containing the winter solstice (Z11). It follows that month 12 must contain Z12, month 1 must contain Z1 and so on. There is therefore a one-to-one relationship between the 12 normal calendar months and the 12 major solar terms. In other words, the solstice rule requires the winter solstice to be in a designated month, and the no zhōngqì rule requires the 12 major solar terms to be in 12 designated months.
In many cases the no zhōngqì rule agrees with the extended rùnyú rule on which months the leap months should be in. This is also not different to understand. Suppose the lunation fraction of a winter solstice in a leap suì is K (usually ≥12/19), which means the conjunction associated with the zǐ month is K lunar cycles before the winter solstice. The major solar term Z12 is Ps/12 = (1 + 7/228)PL after the winter solstice, which is (1 + K + 7/228) after the zǐ month conjunction and (K + 7/228) lunar cycles after the conjunction associated with the second month in the suì. Similarly, the major solar term Z1 is (K + 7/228 + 7/228) lunar cycles after the conjunction associated with the third month in the suì. Note that these numbers are the same as the accumulated values of lunation fraction in the extended rùnyú rule. Suppose the number is equal to or greater than 1, say with solar term Z8. This means that Z8 is equal to or more than one lunar cycle away from the month following the Z7 month (Z7 month means the month containing Z7). In other words, the month following the Z7 month does not contain a major solar term and so is a leap month. This is also the leap month assigned by the extended rùnyú rule. The two rules disagree when the number is very close to 1 so that a major solar term might end up falling on the same day as the lunar conjunction after it, which results in a leap month occurring one month earlier than the extended rùnyú rule.
In the sìfēn system, 19 solar cycles = 235 lunar cycles. There are 19×12=228 major solar terms in 19 years. Since 235=228+7, there are usually 7 months in a zhāng cycle that do not contain a major solar term. Therefore, the no zhōngqì rule usually have 7 leap months in a zhāng cycle. I say "usually" because 19 solar cycles have 6939.75 days, which is not an integer number of days. Hence it's possible to have a winter solstice occuring later than the conjunction but falling on the same day, which could mess up the counting. A bù cycle has integer number of days, so it's guaranteed that there are exactly 28 leap months in 76 years.
There is no historical record to suggest whether or not the no zhōngqì rule was implemented before 104 BCE. However, the no zhōngqì rule was the intercalation rule in the Chinese calendar for more than 2000 years since 104 BCE. In 1645, it was decided that the 24 solar terms were to be computed using the dínqì method, which takes into account the non-uniform motion of the Sun. The no zhōngqì rule needs to be modified in order to account for the fact that a month without a major solar term might appear in a normal suì and more than one month can have no major solar term in a leap suì. These were impossible when the solar terms were defined using the pínqì rule. The current intercalation rule is that there is no leap month in a normal suì no matter whether or not there is a month without a major solar term. In a leap suì, the leap month is placed in the first month after the winter solstice that does not contain a major solar term. If the solar terms are computed using the pínqì rule, there cannot be a month without a major solar term in a normal suì, and exactly one month without a major solar term in a leap suì. The current rule reduces to the no zhōngqì rule in this case. So the current rule can be regarded as a generalization of the no zhōngqì rule.
In this section I use two examples to demonstrate the computation of the ancient six calendars using the solstice rule and no zhōngqì rule. For convenience, I use Ny to denote the calendar year whose New Year day was closest to Jan. 1 in year y in the proleptic Julian calendar, and Sy to denote the suì whose first day was closest to Jan. 1 in year y. Since the New Year days of the six calendars are in general different, Ny refers to different time periods for the six calendars. For example, N-325 began on Dec. 19, -326 and ended on Dec. 7, -325 for the Zhou calendar; N-325 began on Dec. 20, -326 and ended on Dec. 8, -325 for the Lu calendar; N-325 began on Feb. 16, -325 and ended on Mar. 5, -324 for the Xia calendar. Sy also refers to different time periods for the six calendars.
Example 1: Calculate all the months in N-386 in the Zhou calendar.
According to equation (4) and Table 2, the Julian day of the winter solstice of the Zhou calendar closest to Jan. 1, -386 was
JD(W(-386))=1721050.5 + 3/4 - 386×(365 + 1/4) = 1580064.5 + 1/4.
The Julian day at noon was 1580065. Using the standard algorithm for converting Julian days to calendar dates (e.g. algorithm by Richards), the Julian day 1580065 corresponds to Dec. 25, -387. The winter solstice of the Zhou calendar occurred 1/4 days past midnight (i.e. 6 o'clock). According to the formulae for converting a Julian day to sexagenary cycle on our sexagenary cycle page, the stem number of the sexagenary cycle on the date of winter solstice is [mod(X,Y) denotes the remainder of X divided by Y]
1 + mod(1580065-1, 10) = 5, and the stem name is wù. The branch number is
1 + mod(1580065+1, 12) = 3, and the branch name is yín. So the sexagenary cycle name is wù yín. For the Zhou calendar, the first month is the month containing the winter solstice. This means that the conjunction associated with the first month was the first conjunction on or before the date of the winter solstice. The conjunction times are given by equation (1) and Table 2. We want to find the largest integer i so that
1683430.5 + i·PL < 1580065.5 ⇒ i=floor(-103365/PL) = -3501.
Here floor(x) denotes the largest integer smaller than or equal to x. Note that 1580065.5 is the Julian day at midnight of the day after the winter solstice. This is to allow the conjunction to occur later than the winter solstice, but no later than the midnight of the next dayfn4. Note also that if -103365/PL is an integer, the result should be subtracted by 1 because we don't want the conjunction to occur at the midnight of the date after the winter solstice. This nuisance can be removed by a numerical trick that will be introduced in the next Section. Having solved for i, we can now compute the conjunction time associated with the New Year day of -386:
JD1=1683430.5-3501×(29+499/940)=1580042.5 + 461/940. The New Year day in the proleptic Julian calendar, calculated using the same method as above, was Dec. 3, -387 and the sexagenary cycle was bǐng chén. The lunar conjunction occurred at 461/940 days past midnight, which was 11:46:13 using the current 24-hour time system. In ancient time, Chinese astronomers did not use decimals for almanac calculations. The fractional part of a day was expressed as a fraction, which was called xiǎoyú (小餘) or fractional day. So 461/940 is the xiǎoyú of the New Year day conjunction. Since the xiǎoyú of a conjunction was always an integer multiples of 1/940, the denominator 940 was often omitted when mentioning the xiǎoyú.
To determine if there was a leap month in N-386 under the solstice rule or no zhōngqì rule, we need to calculate the number of months between month 1 of N-386 and month 1 of N-385. Note that S-386 and N-386 are the same for the Zhou calendar. The Julian day of the winter solstice in N-385 was
JD(W(-385)) = JD(W(-386)) + 365 + 1/4 = 1580430.
The winter solstice was at noon. The Julian day of the next midnight was 1580430.5. If there was no leap month in N-386, the New Year day conjunction of N-385 would occur 12PL after the New Year day conjunction of N-386. If there was a leap month, it would be 13 PL after the New Year day conjunction of N-386. The Julian day 13PL after JD1 was
JD1 + 13PL = 1580426.5 + 368/940 < 1580430.5.
This means that the month associated with the conjunction at JD1 + 13PL contained the winter solstice and was the first month in N-385. We conclude that there was a leap month in N-386. The solstice rule would place the leap month after month 12. The no zhōngqì rule would place it in the month without a major solar term, which can be determined by computing the major solar terms and lunar conjunctions in N-386. The Julian days of the major solar terms after the winter solstice can be computed by equation (5) or by simply adding integer multiples of Ps/12 to JD(W(-386)). Similarly, the Julian days of the conjunction times after JD1 can be computed by adding integer multiples of PL to JD1. The results are given in the following table.
| JD(conj)-1580000.5 | JD(maj.sol.term)-1580000.5 |
|---|---|
| 42 (month 1) | |
| 64 (Z11, winter solstice) | |
| 72 | |
| 94 (Z12) | |
| 101 | |
| 125 (Z1) | |
| 131 | |
| 155 (Z2) | |
| 160 | |
| 186 (Z3) | |
| 190 | |
| 216 (Z4) | |
| 219 | |
| 246 (Z5) | |
| 249 | |
| 277 (Z6) | |
| 278 | |
| 307 (Z7) | |
| 308 | |
| 337 | |
| 338 (Z8) | |
| 367 | |
| 368 (Z9) | |
| 396 | |
| 399 (Z10) | |
| 426 (month 1) | |
| 429 (Z11, winter solstice) |
Here JD(conj) is the Julian day at midnight on the day of a conjunction, JD(maj.sol.term) is the Julian day at midnight on the day of a major solar term. Subtracting them by 1580000.5 is to make the numbers smaller. From the table, the month associated with JD(conj)-1580000.5 = 308 did not contain a major solar term. It was the 9th month after month 1 and may be labelled as leap month 9. The following table lists the conjunction dates associated with the months in N-386 in the Zhou calendar. The two intercalation rules have exactly the same conjunction dates, but the month labels are different.
| Month (sol.) | Month (n.z.) | No. of Days | Conj. Date | Xiǎoyú |
|---|---|---|---|---|
| 1 | 1 | 30 | Dec. 3, -387 (Bǐng Chén) | 461 |
| 2 | 2 | 29 | Jan. 2, -386 (Bǐng Xū) | 20 |
| 3 | 3 | 30 | Jan. 31 (Yǐ Mǎo) | 519 |
| 4 | 4 | 29 | Mar. 2 (Yǐ Yǒu) | 78 |
| 5 | 5 | 30 | Mar. 31 (Jiǎ Yín) | 577 |
| 6 | 6 | 29 | Apr. 30 (Jiǎ Shēn) | 136 |
| 7 | 7 | 30 | May 29 (Guǐ Chǒu) | 635 |
| 8 | 8 | 29 | June 28 (Guǐ Wèi) | 194 |
| 9 | 9 | 30 | July 27 (Rén Zǐ) | 693 |
| 10 | leap 9 | 29 | Aug. 26 (Rén Wǔ) | 252 |
| 11 | 10 | 30 | Sep. 24 (Xīn Hài) | 751 |
| 12 | 11 | 29 | Oct. 24 (Xīn Sì) | 310 |
| leap | 12 | 30 | Nov. 22 (Gēng Xū) | 809 |
The number of days in a month is determined by the number of days between two successive conjunction dates. As mentioned above, the xiǎoyú of the conjunction is the conjunction time from midnight expressed as a fraction of a day. The denominator 940 is often omitted. Since the lunar cycle is (29 + 499/940) days. The xiǎoyú of a conjunction increases by 499 (mod 940) every month. If the xiǎoyú is smaller than 441, adding 499 to it will still be smaller than 940 and the number of days in the month is 29. If the xiǎoyú is equal to or greater than 441, adding 499 to it will make the conjunction time at or past midnight, and the conjunction will be on the next day. There will be 30 days in the month in this case. Perhaps it is easier to understand this using the 24-hour time system we are currently using. The lunar cycle is 29 days 12 hours 44 minutes and 26 seconds. The time of conjunction from midnight increases by 12 hours 44 minutes and 26 seconds (modulo 24 hours) every month. If the conjunction time is earlier than 11:15:34, adding 12 hours 44 minutes and 26 seconds will still be less than 24 hours and there will be 29 days in the month. If the conjunction time is later than 11:15:34, adding 12 hours 44 minutes and 26 seconds will make the conjunction past midnight and be on the next day. There will be 30 days in the month in this case.
Example 2: Calculate all the months in N-386 in the solstice version of the Xia calendar.
Using equation (4) and Table 2, we find the Julian day of the winter solstice in the suì S-386 was
JD(W(-386))=1721053.5 + 3/4 - 386×(365 + 1/4) = 1580067.5 + 1/4,
which was on Dec. 28, -387 and the sexagenary day was xīn sì. Both the solstice rule and no zhōngqì rule designate month 11 to be the month containing the winter solstice. The conjunction times are given by equation (1) and Table 2. We want to find the largest integer i so that
1883590.5 + i·PL < 1580068.5 ⇒ i=floor(-303522/PL) = -10279.
Having find i, we can now calculate the Julian day of the conjunction associated with month 11:
JD1 = 1883590.5 - 10279PL = 1580042.5 + 359/940.
The xiǎoyú was 359 (omitting the denominator 940). Julian day 1580042.5 corresponds to Dec. 3, -387 and the sexagenary day was bǐng chén. To determine if there was a leap month in S-386, we can compare floor(JD(W(-385))+1.5) and floor(JD1+13PL+0.5) and see which of them is larger. Adding 0.5 to the Julian day is to measure time from midnight instead of noon.
floor(JD(W(-385))+1.5) = floor(1580067.75+365.25+1.5)=1580434,
floor(JD1+13PL+0.5)=floor(1580042.5 + 359/940 + 13×(29 + 499/940) + 0.5) = 1580427 < 1580434,
which means that there was a leap month in S-386. The solstice rule would place the leap month after month 12 and so month 1 was the third month after month 11. Since this New Year day was closest to Jan. 1, -386, it was the New Year day of N-386 by definition. Thus the leap month was in N-387 and there was no leap month in N-386. The no zhōngqì rule would give a different result. To see that, we have to find out the month without a major solar term in S-386. Using the same method as in the previous example, I find that the month without a major solar term was the fifth month after month 11, making it in N-386. The first month was then the second month after month 11 and the leap month was the month after month 3. The following table summarizes the result.
| Month (sol.) | Month (n.z.) | No. of Days | Conj. Date | xiǎoyú |
|---|---|---|---|---|
| leap* | 1 | 29 | Jan. 31, -386 (Yǐ Mǎo) | 417 |
| 1 | 2 | 30 | Mar. 1 (Jiǎ Shēn) | 916 |
| 2 | 3 | 30 | Mar. 31 (Jiǎ Yín) | 475 |
| 3 | leap 3 | 29 | Apr. 30 (Jiǎ Shēn) | 34 |
| 4 | 4 | 30 | May 29 (Guǐ Chǒu) | 533 |
| 5 | 5 | 29 | June 28 (Guǐ Wèi) | 92 |
| 6 | 6 | 30 | July 27 (Rén Zǐ) | 591 |
| 7 | 7 | 29 | Aug. 26 (Rén Wǔ) | 150 |
| 8 | 8 | 30 | Sep. 24 (Xīn Hài) | 649 |
| 9 | 9 | 29 | Oct. 24 (Xīn Sì) | 208 |
| 10 | 10 | 30 | Nov. 22 (Gēng Xū) | 707 |
| 11 | 11 | 29 | Dec. 22 (Gēng Chén) | 266 |
| 12 | 12 | 30 | Jan. 20, -385 (Jǐ Yǒu) | 765 |
* This was a leap month in N-387.
In the previous section, I use fractions to do calendar calculation. The main reason is to introduce the concept of xiǎoyú, a term often appears in books and literature. Modern calculations are usually done on a computer. Although fractions are better in terms of computational efficiency, it is more complicated to write a program to handle fractions. That's why all calendar calculations on this website are done by using floating point numbers. The solar cycle is represented by the number 365.25 and the lunar cycle by 29.53085106382979. However, there is one thing we should be careful. When the xiǎoyú of a conjunction is exactly 0, the conjunction occurs exactly at midnight. The decimal part of the Julian day is exactly 0.5, but floating point roundoff error may give 0.49999999999 instead, resulting in an off-by-one-day error. This can be prevented by adding 0.0001 to the Julian days in Table 2. The xiǎoyús of conjunctions in the ancient six calendars are always integer multiples of 1/940 ranging from 0 to 939/940. After adding 0.0001, all of the xiǎoyús are shifted by 0.094/940. It is now impossible for the xiǎoyú to be exactly 0 and the floating point roundoff error will never produce a one-day error. Since the conjunctions can no longer occur at midnight, the nuisance mentioned in Example 1 in the previous Section is gone.
Now that the computation is done using decimals, it is no longer necessary to calculate the xiǎoyú. We can still calculate it if we want to:
xiǎoyú = JD + 0.5 - floor(JD + 0.5) - 0.0001.
The last term is to remove the 0.0001 added to JD. The xiǎoyú in the above equation is given in decimals. If we know it is an integer multiples of 1/940, we can easily calculate the numerator:
xiǎoyú × 940 = floor(940 ( JD + 0.5 - floor(JD + 0.5) )
Since 0.0001 is added to the JD, 940 ( JD + 0.5 - floor(JD + 0.5) is some integer plus 0.094. The floor() function simply removes the decimals.
The lunation fraction of a solar term is also easy to calculate. Suppose JD is the Julian day of a solar term. Then
L = (JD - JD(M0))/29.53085106382979
lunation fraction = L - floor(L)
The appropriate value of JD(M0) can be found in Table 2 for each of the ancient six calendars. Here L is the time difference between the solar term and the conjunction M0 at the calendar epoch in units of lunar cycles, i.e. the number of lunations from M0 to the solar term. By definition, the lunation fraction of a solar term is the time from its previous conjunction in units of lunar cycles, which is simply the fractional part of L. If L is negative, the lunation fraction will be 1 - decimal part. Since floor(L) returns the largest integer smaller than or equal to L, the above formula is also valid for negative value of L.
Footnotes and References
[fn1] It seems strange that one would assume a solar term and lunar conjunction occurring at the same time because we now know that the orbital periods of the Earth and Moon are not commensurate with each other. Their motions are not dynamically locked like some other objects in the solar system. The ratio 235:19 used by the sìfēn system is only an approximation. It is therefore almost impossible for a solar term and conjunction occurring at the same time, let alone both occurring at midnight. Of course, the ancient people didn't know that. Besides, the concept of winter solstice and conjunction was not rigorously defined. Winter solstice simply referred to the day when the shadow cast by the Sun at solar noon was the longest. Even if the concept were defined rigorously, the instruments at that time would probably only allow them to measure the time to an accuracy of about a day, with the exception that the conjunction time could be measured more accurately during a solar eclipse. Of course, we can interpret the time coincidence statement merely means that the time difference between a particular solar term and conjunction is less than about a day. That the times were assumed to be the same was just for convenience of calculations. A more likely explanation is that the calendar makers were greatly influenced by the "mandate of heaven" political doctrine of the time.
[fn2] Astronomical conjunctions are calculated by the modern method. That is the method described in this pdf document, but precession has to be calculated using the Vondrák et. al. precession model described in Section 7.2 of the document. The computed TDB times are then converted to UT1 using the method described in Section 8 of the document. Julian days JD(Mi) of the calendrical conjunctions are calculated using equation (1) above. The resulting times are regarded as the local times and have to be converted to UT1 for comparison with the astronomical conjunction times. The Zhou calendar was used by the Zhou dynasty whose capital was at the present-day Luoyang. The longitude of Luoyang is λ=112.45°E and its local time is (112.45/360) days ahead of UT1, so (112.45/360) days have to be subtracted from JD(Mi) to convert from local time Julian day to UT1 Julian day. Three other relevant longitudes are λ=116.98°E (present-day Qufu) for the Lu calendar, λ=108.9°E (present-day Xi'an) for the Zhuanxu calendar, λ=114°E (present-day Kaifeng) for the Xia calendar. I don't know which states used the Huangdi and Yin calendars, and I use λ=114°E to represent the approximate longitudes of places that might have used these calendars. The differences between the local times of the states in the Warring States period were less than one hour and so the results will not change much if a different longitude is used.
[fn3] In the three books Tables of Chinese Calendars in the Pre-Qin Period, 3500 Years of Calendars and Astronomical Phenomena, and Ancient Chinese Calendars and Almanacs, Zhāng Péiyú wrote that the Yin calendar designates the zǐ month as the beginning of a year, which is at odds with the commonly accepted notion. He did not explain or justify his statement.
[fn4] For the rùnyú rule, we would want to use the Julian day of the winter solstice 1580064.5 + 1/4 = 1580064.75 and require
1683430.5 + i·PL ≤ 1580064.75.
Note the ≤ instead of < to take into account the possibility of the winter solstice and conjunction occurring at the exact same time.[Zhang87] Zhāng, Péiyú (張培瑜), Zhōng Guó Xiān Qín Shǐ Lìbiǎo (《中国先秦史历表》 or Tables of Chinese Calendars in the Pre-Qin period), Shandong Qilu Press, June 1987.
[Zhang97] Zhāng, Péiyú (張培瑜), Sānqiān Wǔbǎiniǎn Lìrì Tiānxiàng (《三千五百年历日天象》 or 3500 Years of Calendars and Astronomical Phenomena), Elephant Press, July 1997.
[ZCBH08] Zhāng, Péiyú (張培瑜), Chén, Měidōng (陳美東), Bó, Shùrén (薄樹人), and Hú, Tiězhū (胡鐵珠), Zhōng Guó Gǔdài Lìfǎ (《中国古代历法》 or Ancient Chinese Calendars and Almanacs), China Science Press (Beijing), March 2008.