古 六 历 的 计 算 方 法
初稿: 2019年3月
本网站的古六历资料是参考张培瑜、陈美东、薄树人和胡铁珠著的《中国古代历法》张陈薄胡书中第三章第六节。该书的前言说书中各章节由四人分别执笔,第三章由张培瑜撰写。张培瑜是中国科学院紫金山天文台的研究员。本网站的计算方法不依书中所述的方法,而是采用一套方便编写计算机程式的方法,计算结果和张培瑜著的《中国先秦史历表》张培瑜87和《三千五百年历日天象》张培瑜97所载历日数据一致。下面会详细介绍具体的计算方法。
古六历是指周历、鲁历、殷历、夏历、黄帝历和颛顼历这六部历法,六历的计算都是用四分术。四分术的名称缘于其岁实(即回归年)取三百六十五又四分之一日(即365.25日),朔策(即朔望月)取岁实的19/235,即
朔策 = (365 + 1/4)日×19/235 = (29 + 499/940)日 = 29.530851064日。
这样做的目的是要使235个朔望月等于19个回归年。由于235=19×12+7,在十九年里加七个闰月就能使历法一年的平均值等于四分术采用的岁实了。所以古六历的六部历法全是采用十九年七闰法。六历不同之处是所选的历元不同。
历元在这里是指历法的起算点,一般是指定某一日某二十四节气(通常是冬至)与合朔发生在同一时刻(通常是夜半,即午夜零时),称之为某节气合朔齐同。注一
以周历为例,周历的历元是指定冬至与朔发生在某甲子日的夜半,即冬至合朔齐同。唐朝以前的历法以平朔法计算合朔时刻、以平气法计算节气时刻,即假设月亮和太阳以均匀速度在天空运行。四分术的岁实=365.25日=(12+7/19)朔策,根据规定在历元时冬至与合朔发生在同一时刻,下一年的冬至便在(12+7/19)个朔望月后,这时冬至与合朔就不齐同了,冬至离之前最接近的合朔有7/19个朔望月(即10.88日),这7/19称为「闰余」。
一般而言,闰余定为某一特定节气(通常是冬至)的月龄,即该节气离之前合朔的时间间隔,月齡可以用日計,也可以用朔策的分數倍表示,此處用朔策的分數倍表示(月龄可以用日计,也可以用朔策的分数倍表示,此处用朔策的分数倍表示)。所以闰余在历元是0,一年后是7/19,容易看出下一年的闰余是这年闰余加上7/19,如果加后超过1,就要减去1。依这法则可算出闰余从历元算起的头十九年是(略去分母19):0、7、14、2、9、16、4、11、18、6、13、1、8、15、3、10、17、5、12,到了第二十年,闰余又回复到0,即冬至与合朔又齐同了,由此可知闰余有十九年的周期。十九年称为一「章」。
一章后虽然冬至与合朔又发生在同一时刻,但这时刻不在夜半,因为365.25×19=6939.75,用现在的时间系统来说,冬至与合朔这时发生在18时,要到四章(76年)后冬至与合朔才会又同时发生在夜半,四章称为一「蔀」。一蔀后虽然冬至和合朔又同时在夜半,但是365.25日×76=27759日,而27759不是60的倍数,所以一蔀后的日干支不是甲子,而是癸未,要到二十蔀(1520年)后才可回复到甲子日冬至和合朔同在夜半,二十蔀称为一「纪」。但是一纪是1520年而1520不是60的倍数,所以一纪后年的干支与历元时不同,要到三纪(4560年)后才可回复与历元相同的年干支,三纪称为一「元」。以下总结四分术的法数。
岁实: 1岁 = (365+1/4)日 = (12+7/19)月
朔策: 1月 = (29 + 499/940)日
章: 19岁 = 235月 = (6939+3/4)日
蔀: 4章 = 76岁 = 940月 = 27759日
纪: 20蔀 = 1520岁 = 18800月 = 555180日
元: 3纪 = 4560岁 = 56400月 = 1665540日
古六历在战国时期创制行用,但是当时的历法已经散失,今天我们可从后来的史藉例如《汉书》、《续汉书》等得知古六历的资料,可是两部书都没有记载六历的历元。直到《开元占经》才给出六历离开元二年(公元714年)的上元积年。所谓上元,是一个理想的历元,其时日月合璧、五星连珠。日月合璧是指太阳和月亮的经度相同,五星连珠是指水、金、火、木、土五行星同时出现在天空同一方的现象,清朝钦天监规定「连珠」指五行星的经度相差小于45度。下表列出《开元占经》的上元积年数据。
| 历法 | 上元积年 | 上元的公历年 | 历元日干支、 气朔关系 |
|---|---|---|---|
| 黄帝历 | 2760863 | -2760149 | 甲子日夜半冬至合朔齐同 |
| 殷历 | 2761080 | -2760336 | |
| 周历 | 2761137 | -2760423 | |
| 夏历 | 2760589 | -2759875 | 夏历有两个版本,其一是甲子日夜半冬至合朔齐同, 另一是甲子日夜半雨水合朔齐同。 |
| 颛顼历 | 2761019 | -2760305 | 己巳日夜半立春合朔齐同 |
| 鲁历 | 2761514* | -2760800 | 甲子日夜半冬至闰余一 |
* 《开元占经》给出的鲁历上元积年是2761334,历代多位学者已发现这数字不正确。表中列出的上元积年是根据张培瑜的推算。
表中「甲子日夜半冬至合朔齐同」又作「甲子朔旦冬至」,是指冬至和合朔同时发生在甲子日的夜半(午夜零时)、「甲子日夜半雨水合朔齐同」或「甲子朔旦雨水」,指雨水和合朔同时发生在甲子日的夜半、「己巳日夜半立春合朔齐同」或「己巳朔旦立春」,指立春和合朔同时发生在己巳日的夜半。上表指出夏历有两个版本,这里称冬至合朔齐同为「冬至版」,称雨水合朔齐同为「雨水版」。
鲁历的情况较为特殊。首先,历代多位学者已指出《开元占经》列出的鲁历上元积年不正确,表一的数据是根据张培瑜的推算。此外,《汉书‧律历志上》说:「鲁历不正,以闰余一之岁为蔀首。」意思是说鲁历的历元和其他五历不同,不是以某节气与合朔齐同,而是以闰余一为历元。「闰余一」其实是闰余是1/19的简略说法。鲁历的历元是冬至发生在甲子日夜半,但是其时冬至的月龄是1/19,所以合朔在甲子日夜半之前1/19个朔策(即1.554日前)。严格来说,鲁历的历元不符合上元的要求,因为当时并非日月合璧。某节气与合朔齐同时,该节气的月龄是0,又称「闰余无」。所以除鲁历外,其他五历的历元都取闰余无。
上元的概念由西汉未年的刘歆提出,推算上元是十分繁琐的同余算数问题。由于日月合璧、五星连珠十分罕见,上元离历法使用的时间(即上元积年)非常遥远,例如南宋李德卿所制《淳佑历》(1250年)取上元积年数为「一亿二千二十六万七千六百七十七」! 积年数大使天文计算十分不便。还有一个弊病是上元算法存在严重的附会情况:上元推算十分繁琐,计算时需要简化,天文常数往往以实测为参照,然后调整数据来配合算出的上元。上元积年的推算从元朝《授时历》起废除,历法计算直接用实测数据。关于上元积年的推算,这里另有专文论述。
《开元占经》载的古六历上元积年,应是东汉时推算附加的,不是战国时采用的历元。用上元为历元计算古六历不方便,应当选取较接近战国时代的历元。从上一节可知,四分术以一纪1520年为日干支、节气合朔夜半齐同的周期,把上元加上1520年的整数倍后得出的历元依然是同一日干支的节气合朔夜半齐同。这里以周历为例,《开元占经》列出的周历上元相当于公元-2760423年,把这年数加上1520×1816=2760320后得出-103年,即公元前104年。所以公元前104年的甲子日夜半冬至合朔齐同也可作为周历的历元,这比-2760423年方便得多。有一点要注意,中国历法是阴阳合历,「阴」的部分跟从月相,「阳」的部分跟从太阳,以冬至作为「阳」的岁首。公元前104年的甲子日冬至其实是最接近公元前104年1月1日的冬至,我们知道这在公元前105年的12月末。只要找出公元前105年的12月末的甲子日便知周历的历元,计算得出的甲子日落在公元前105年的12月25日。
历元的选取当然不一定总是要求日干支与上元时相同,把历元加上蔀(76年)的整数倍后,得到的年份依然是节气与合朔与上元有相同关系。以周历为例,把-103年减去76年的三倍得到-331年。也就是说周历在前332年冬至和合朔同在夜半,但是76年×3=228年=83277日,不是60日的倍数,故前332年的历元日干支不是甲子,而是甲子日之前83277日,用同余算术可算出是丁卯日。前332年丁卯冬至在前333年12月25日,其时周历的冬至和朔同时在夜半。前104年和前332年都可称为周历的「蔀首」,蔀可用日干支为名,例如前104年是周历的甲子蔀首、前332年是丁卯蔀首。某年与蔀首的积年加一称为该年的「入蔀年」,例如前331年入周历丁卯蔀二年。
古六历的六部历法各有不同的历元,也就是说六历有不同的历法起算点,这在编写计算机程式上不方便。这里介绍一个统一方法计算古六历。
这方法是用儒略日数计算合朔和节气时刻。儒略日数是从公元前4713年1月1日正午起算的日数,用儒点日数就是把六历的时间起算点统一在公元前4713年1月1日正午。以周历为例,上节说根据周历历法,公元前105年12月25日冬至和合朔同时发生在夜半,公元前105年12月25日夜半的儒略日数是1683430.5。根据平朔和平气法,周历的冬至和合朔时刻的儒略日数可用以下公式计算。
JD(Mi) =1683430.5 + i·PL
JD(W(y)) = 1683430.5 +(y+103)·Ps
这里PL=(29+499/940)日是四分术的朔策,Ps=365.25日是四分术的岁实。Mi指从公元前105年12月25日合朔算起的第i个合朔;W(y)是最接近公历y年1月1日的冬至,在战国时代总是发生在公元y-1年的12月末。
古六历其他历法的冬至和合朔时刻也可以用类此公式计算:
JD(Mi) = JD(M0) + i·PL (1)
JD(W(y)) = JD(W(y0)) + (y-y0)·Ps (2)
这里i指从历元合朔M0算起的积月,JD(M0) 、JD(W(y0)) 和y0的数值由下表给出。计算冬至的公式中,可以把JD(W(y0))和y0结合成另一参数:
JDW=JD(W(y0)) - y0·Ps (3)
冬至的公式便可简化成
JD(W(y)) = JDW + y·Ps (4)
下表把参数JDW列在最后一栏。
| 历法 | JD(M0) | JD(W(y0)) | y0 | JDW |
|---|---|---|---|---|
| 黄帝历 | 1783510.5 | 1783510.5 | 171 | 1721052.5 + 1/4 |
| 殷历 | 1704250.5 | 1704250.5 | -46 | 1721051.5 + 1/2 |
| 周历 | 1683430.5 | 1683430.5 | -103 | 1721050.5 + 3/4 |
| 夏历(冬至版) | 1883590.5 | 1883590.5 | 445 | 1721053.5 + 3/4 |
| 夏历(雨水版) | 1883650.5 | 1883589.5 + 1/8 | 445 | 1721052.5 + 7/8 |
| 颛顼历 | 1726575.5 | 1726529.5 + 11/32 | 15 | 1721050.5 + 19/32 |
| 鲁历 | 1545728.5 + 419/940 | 1545730.5 | -480 | 1721050.5 |
这些参数的计算方法是首先把上元的年份加上一纪(1520年)的整数倍使之接近战国时代的年份,这样便得到y0,然后找出对应历元日干支的公历日期。日干支以六十日为周期,因为我们知道节气的大约公历日期(冬至:12月末、立春:2月初、雨水:2月末),所以不难找到历元日干支的公历日期,最后把公历日期转化为儒略日数。
黄帝历、殷历、周历和冬至版夏历的历元都是夜半冬至合朔齐同,所以JD(M0)=JD(W(y0))。雨水版夏历以雨水合朔齐同为历元,而雨水是冬至后第四个二十四节气,根据平气法,冬至在雨水之前(4/24)个岁实=60.875日,所以JD(W(y0))=JD(M0)-60.875。颛顼历以立春合朔齐同为历元,立春是冬至后第三个节气,冬至在立春之前(3/24)个岁实=(45+21/32)日,所以JD(W(y0))=JD(M0)-(45+21/32)。鲁历以冬至闰余一为历元,所以JD(M0)=JD(W(y0))-(1/19)×(29+499/940)。
我们虽然不知道战国时代是不是已经创立了全部二十四节气,但是仍可用平朔法把岁实分成二十四等份计算从公元y-1年冬至算起的各节气儒略日数:
JDq(j,y) = JD(W(y)) + (j/24)·Ps (5)
这里j是从冬至算起的节气数,以j=0表示冬至、j=1表示小寒、j=2表示大寒、j=3表示立春……j=23表示大雪(二十四节气的名称和次序可参阅本网站的二十四节气网页)。公式(5)中除了冬至落在y-1年的12月末外,其余节气都在公元y年。
用儒略日数的好处是已有标准方法把儒略日数转换成公历日期,本网站的干支网页也有用儒略日数计算日干支的公式。
公式(1)、(4)和(5)也有助我们对古六历的了解。六历都采用平朔和平气法,所以合朔时刻是某常数加上朔策的整数倍,节气时刻是某常数加上岁实/24的整数倍。六历都采用四分术,所以朔策PL和岁实Ps的数值相同。六历之不同,在于参数JD(M0)和JDW取不同的数值而已,当然,这说法等同于「六历的历元不同,历元气朔的关系也不尽相同」。
四分术岁实365.25日和儒略历相同,比回归年大0.0078日,累积128年会有一日偏差。朔策(29+499/940)日比朔望月的平均值大0.000268日,累积3730月(约三百年)会有一日偏差。六历所取的参数不同,除了观测数据可能有差异外,很可能还与历法制定的时间不同有关。下图显示历法合朔和实际合朔之差,图中所见之波动是因为用平朔法计算合朔只计及 月亮和太阳的平均运动。除了波动外可明显看出时间差异平稳增长,和预期的结果一致。两合朔时刻之差的平均值可以取数个波动之平均值而得,更方便的方法是用线性回归法拟合数据而求得一直线。我们知道两朔时刻之差的增长是因为四分术的 朔策比朔望月的平均值稍长而造成的,时刻差异是时间的线性函数,所以用线性回归是恰当的。历法之朔早于实际合朔称为「先天」,迟于实际合朔称为「后天」。从下图可见周历、黄帝历和冬至版夏历在整个战国时代大多数时间是先天的,而其余历法有某一年份最为合天,该年份以前大多先天,该年份以后则大多后天。雨水版夏历在公元前460年左右最为合天,鲁历在前450年左右最为合天,殷历在前435年左右最为合天,颛顼历在前335年左右最为合天。
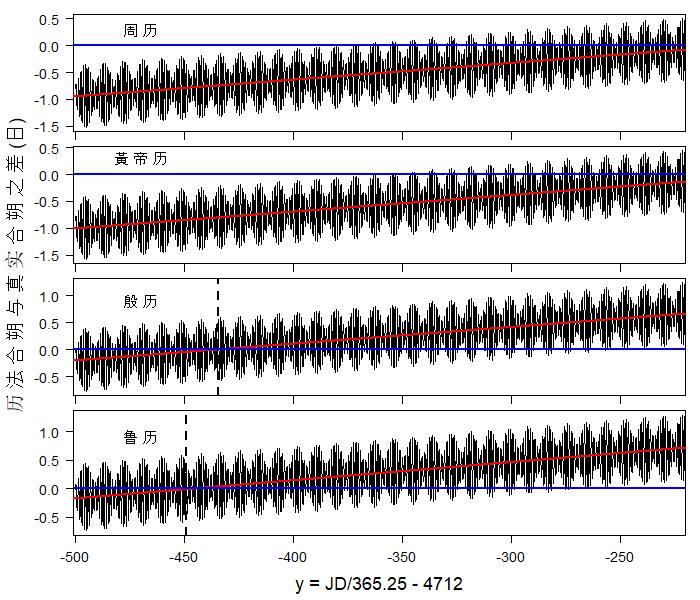
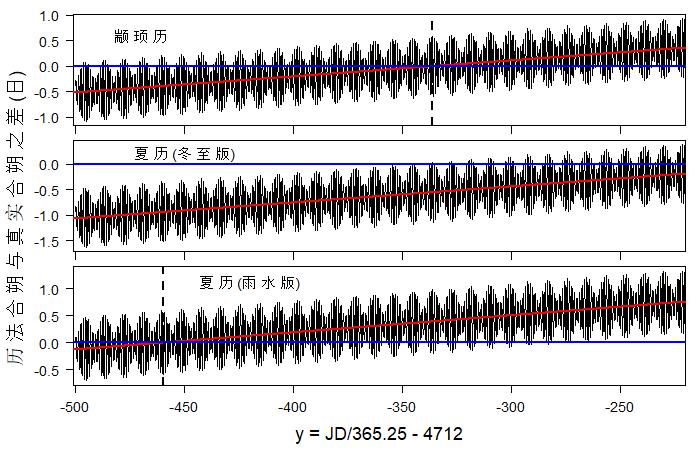
周历、鲁历、黄帝历都以建子(即含冬至的月份,现在的十一月)为年首,两个版本的夏历都以建寅(现在的正月)为年首,殷历以建丑(现在的十二月)为年首注三,颛顼历则以建亥(现在的十月)为年首。除了颛顼历外,各历法的月序都是正月、二月、三月……十二月。闰月的情况下一节再说。由于月建不同,夏历的正月往往在周、鲁、黄帝历的正月之后两个月。颛顼历的月序比较特别,起始月不称正月而是依夏历称建亥为十月,颛顼历的月序是十月、十一月、十二月、正月、二月……九月。
目前学界对于古六历的置闰法则未有一致意见,对于闰月位置也没有一致意见。置闰方法有三种说法:闰余法、固定冬至法和无中气法;闰月位置有人主张置于年终,称为闰月而不用注明闰几月,但也有人主张可以在年中置闰。对于颛顼历的闰月位置,因为有较多的资料争议比较少,一般认为闰月置于年终,称为后九月。
下面三小节简单介绍闰余法、固定冬至法和无中气法。无中气法的规则必然会出现年中闰月,固定冬至法一般把闰月置于年终,闰余法却没有指明一定要在年终或年中置闰。本网站的的年历网页和朔闰表网页计算古六历时效法张培瑜著的《中国先秦史历表》张培瑜87和《三千五百年历日天象》张培瑜97,采用固定冬至法并把闰月置于年终,但也有注明无中气的月份以供参考。
周历和黄帝历都以建子含冬至的月份为年首,也都以冬至合朔齐同作为蔀首,这里就先以这两部历法为例说明闰余法。
四分术的岁实=(12+7/19)朔策,如上所述,闰余在一年后增加7/19,如果超过一,则把一减去。二历在蔀首的第一年闰余是0,即冬至在正月初一夜半,下一年冬至在一个岁实后,在12个月后加7/19朔策,闰余是7/19,如果没有闰月,冬至在正月十二。再过一年后,闰余是14/19,如果没有闰月,冬至在正月廿三。14/19加上7/19超过一,意味着下一年的冬至在这一年的正月后十三个月,假如这一年还是不闰,下一年冬至便会在二月,而正月不含冬至,月建不再是建子了。所以为了使正月的月建是建子,第三年必须有闰月,使冬至在第四年仍在正月,闰余是2/19。不难看出,如果某年的闰余加上7/19后达到或超出一,该年必须有闰月才能使正月月建保持在建子。所以闰余法的置闰法则是:在冬至的月龄达到或超过12/19的年份加插闰月。由入蔀年的第一年闰余零起算,闰余在本文第一节「四分术的朔策和岁实」已一一列出,从中可见须要置闰的年份是第三、六、九、十一、十四、十七和十九年。到了第二十年,闰余回复到零,所以闰月有十九年的周期,即章周。这闰余法得到的闰年规律是3-3-3-2-3-3-2,意思是闰月出现在第三年,然后是第六(=3+3)年,然后是第九(=3+3+3)年,然后是第十一(=3+3+3+2)年等等。
鲁历同样以建子为正月,只是以闰余一为蔀首,从本文第一节「四分术的朔策和岁实」的闰余数值可见,这其实是把章周的起算年放在以闰余无为蔀首的第十一年,所以有闰月的年份变成第三、六、八、十一、十四、十七和十九年。
其余三历不以建子为年首,置闰法则可修改为:在冬至的月龄达到或超过12/19之岁加插闰月。此处「岁」是指从建子月初一日到下一个建子月之前一日的那段时间。「岁」与「年」在周历、黄帝历和鲁历是相同的。这置闰法则会使冬至在殷历固定在十二月、在冬至版夏历固定在十一月、在雨水版夏历和在颛顼历则只可说大致在十一月。殷历和冬至版夏历都以闰余无为蔀首,置闰之岁与周历和黄帝历一致。雨水版夏历以雨水合朔齐同为蔀首,冬至在雨水之前(1/6)岁实=(2+7/114)朔策,由此推出蔀首冬至的月龄是107/114,其后十八岁的冬至月龄是(略去分母114):35、77、5、47、89、17、59、101、29、71、113、41、83、11、53、95、23、65,置闰之岁是第一、三、六、九、十二、十四和十七岁。颛顼历以立春合朔齐同为蔀首,冬至在立春之前(1/8)岁实=(1+83/152)朔策,由此推出蔀首冬至的月龄是69/152,其后十八岁的冬至月龄是(略去分母152):125、29、85、141、45、101、5、61、117、21、77、133、37、93、149、53、109、13,置闰之岁是第二、五、七、十、十三、十六和十八岁。
闰余法只规定哪一岁须要置闰,但没有规定闰月的位置,闰月可以置于年终也可以置于年中。年终置闰很简单,不必细说,现在谈谈年中置闰的法则。如上述,当冬至的月龄达到或超过12/19时须要置闰。每岁的冬至月龄增加7/19,将此数除以12得7/228,把这一岁的冬至月龄在建子月后每月加上7/228,则在十二个月内必然会达到或超过一,闰余的年中置闰法则是以累积月龄数刚刚达到或超过一的那个月作为闰月。
鲁历、雨水版夏历和颛顼历相对于蔀首的置闰之岁虽然和其余古六历不同,但是只要改变起算之岁,就可以得到其余六历的相同置闰之岁次序,也符合3-3-3-2-3-3-2的规律。节气的月龄有一章(十九年)的周期,所以用闰余法得出的闰月也有十九年的周期。这当然是因为四分术的岁实和朔策有19岁实=235朔策的关系, 235=19×12+7,所以十九年要置七个闰月。当然,最简单的置闰法则是把7个闰月均匀放在235个月之间。这样,闰月应出现在第(235j/7)个月(j=1、2、3、4、5、6、7),取最接近的整数,便得出闰月应置于第34、67、101、134、168、201和235个月,而这些月份落在第三、六、九、十一、十四、十七和十九岁,正是3-3-3-2-3-3-2的规律。周历、殷历、黄帝历和冬至版夏历都是以冬至合朔齐同作历元,用闰余年中置闰法得出四历的闰月出现在第34、68、101、135、168、202和235个月,和上述闰月均匀安排基本上相同,两者的差异是由于闰余年中置闰法要求月龄累积数达到或超出一才置闰,所以与均匀置闰取最接近(235j/7)的整数不同,如果取不小于(235j/7)的最小整数就没有差异了。其余历法的年中闰月位置不同,是由于月数的起算点不同而已。
这法则是以冬至固定在某个特定的月份内的原则决定要不要置闰,冬至固定的月份以历法年首的月建决定。周历、鲁历、黄帝历都以建子为正月月建,所以冬至固定在正月;殷历以建丑为正月,冬至固定在十二月;夏历以建寅为正月,冬至固定在十一月;颛顼历虽然以建亥为年首,但采用夏历的月序,所以冬至也是固定在十一月。
如前述,「岁」是指从建子月初一日到下一个建子月之前一日的那段时间。一岁可以有十二个月,也可以有十三个月。这里称含十二个月的称为「平岁」,含十三个月称为「闰岁」。由于固定冬至法规定建子月必定是某个特定月份,闰岁那十三个月中必定要有闰月,闰月置于年终,而平岁则没有闰月,这就是固定冬至法的置闰规则。潜规则是一岁必须有十二个正常月而且每个常月只能出现一次。
固定冬至法在很多情况下所得的闰月年份和闰余法一致,其实这也不难理解。四分术的岁实=(12+7/19)朔策,如果某岁冬至的月龄是K,建子月的朔在冬至之前K个朔策,下一岁的冬至在建子月朔后(12+K+7/19)个朔策,如果K<12/19,下一岁冬至在建子月后不足十三个月,所以下一个建子月一般在该岁建子月后的第十二个月,也就是说两建子月相差十二个月,是平岁而没有闰月;如果K≥12/19,下一岁冬至在建子月后一般会超过十三个月,这时两建子月相差十三个月,所以就有闰月。结果与闰余法则一致。但是这只是一般的情况,有时会有例外。下面以颛顼历为例说明。
根据上面计算的颛顼历冬至月龄,在入蔀第十五岁的月龄是93/152<12/19,按闰余法这岁没有闰月,下一岁(即入蔀第十六岁)的冬至月龄是149/152>12/19,按闰余法这岁须置闰。入蔀第十六岁的冬至离十一月朔有149/152朔策,也就是说在十二月朔之前3/152个朔策,即13小时59分18秒。如果十二月朔发生在13:59:18以后,则冬至与十二月朔发生在同一日。计算得出十二月朔的时刻在16:14:18,而冬至在同日2:15。也就是说根据闰余法入蔀第十六岁的冬至在十二月初一,这是固定冬至法不允许的。中国历来以子正(午夜零时)作为一日的起始时刻,虽然十二月朔的时刻迟于冬至时刻,但是冬至与朔仍然视为同在一日。固定冬至法规定颛顼历冬至必须在十一月,所以那个迟冬至约14小时的朔只能是十一月朔,这样一来入蔀第十五岁的十一月和入蔀第十六岁的十一月相差十三个月,所以按固定冬至法颛顼历的入蔀第十五岁要置闰;入蔀第十六岁的十一月和入蔀第十七岁的十一月只差十二个月而不设闰月。这与闰余法规定的置闰之岁不同,可见固定冬至法和闰余法有时会有差异。
从上面例子可以看出,一般而言如果冬至月龄非常表近一的时候,有可能会出现冬至与冬至之后的合朔相差少于一日而同在一日,这时闰余法和固定冬至法就会有差异。对于周历、鲁历、黄帝历、殷历和冬至版夏历,冬至的月龄在0和18/19之间,也就是说冬至和其后的合朔相差大于1.55日,不可能出现冬至和其后的朔同在一日的情况,用闰余法和固定冬至法计算此五历会得出相同的结果。
无中气法也是把冬至固定在某个特定的月份,如果两个建子月相差十二个月(平岁)则不闰,相差十三个月(闰岁)则闰。无中气法对闰月的位置有明确规定:闰月置于无中气的月份。
如节气网页所述,中气是指由立春算起双数的节气,即雨水、春分、谷雨、小满、夏至、大暑、处暑、秋分、霜降、小雪、冬至、大寒。根据平气法两中气的时间间隔是岁实的十二分之一,用四分术的岁实得(30+7/16)日。由于时间相差大于三十日,一个月最多只能有一个中气。一岁有十二个中气,平岁有十二个月,由此可知每月含一个中气。闰岁有十三个月,但只有十二个中气,由此可知有一个月(而且只能有一个月)不含中气,无中气法就把这个唯一不含中气的月份定为闰月。因为把冬至固定在某个特定的月份,而闰月不含中气,所以非闰月的月份含的中气也固定。以夏历为例,冬至之月(建子)固定在十一月,从而推出十二月必含大寒、正月必含雨水、二月必含春分等。这样月份与中气有一一对应的关系。换言之,固定冬至法把冬至固定在指定的月份,无中气法把十二个中气固定在指定的十二个月份。
用无中气法得出的闰月和用闰余之年中置闰法的结果大致相同,这也不难理解。假设某岁冬至的月龄是K,建子朔就一般在冬至之前K个朔策。两中气相隔岁实/12=(1+7/228)朔策,故大寒在冬至之后(1+7/228)朔策,在建子朔后(1+K+7/228)朔策,在建子朔算起的第二个朔后(K+7/228)朔策。同理,雨水在建子朔算起的第三个朔后(K+7/228+7/228)朔策,余类推。这规律与闰余年中置闰的月龄累加法相同。当累加之和刚刚达到或超过一的时候就意味着会有一个中气离开前一中气之月之后的那一个月超过一个朔策,也就是说前一中气之月之后的那一个月不含中气,所以是闰月。但是当累加之和很接近一时,中气与其后的朔可能会同在一日,这时该中气归其后之朔的月份,之前的月份就不含中气而定为闰月,这闰月便会和闰余年中置闰法有一个月之差。所以无中气法和闰余年中置闰法有时会有差异。
四分术的19岁实=235朔策,19岁有19×12=228个中气,228=235-7,所以一章(十九年)一般有七个无中气月,但有可能出现合朔迟于中气但在同一日的情况,这可能会使闰月偏离十九年七闰的规律。一蔀(76年)后节气与合朔的关系与历元一致,所以无中气法必定符合七十六年二十八闰的规律。
史书并没有记载无中气法在汉朝以前是否使用过,但是自汉武帝太初元年(公元前104年)开始在其后的一千七百多年中,无中气法一直是中国历法的置闰标准。直到清顺治二年(1645年)改用定气计算节气后,置闰法则才须要略加修改以应付平岁可出现无中气月、闰岁可出现两个无中气月这些平气法不可能出现的现象。现在农历的置闰法则是平岁无论有没有无中气月都不置闰,闰岁则把闰月置于冬至后第一个无中气的月份。用平气法计算二十四节气,平岁不可能出现无中气月,闰岁只有一个无中气月,所以现行置闰法则用于平气节气得出的结果和无中气法完全相同,可说是无中气法的推广法则。
这里以两个例子展示用固定冬至法和无中气法计算古六历。为方便起见,下面用Ny表示历年年首最表近公元y年1月1日的历年,用Sy表示最表示岁首最接近公元y年1月1日的岁。由于六历的年首月建和朔日都不尽相同,Ny对于各历指不同的时段。例如周历的N-325始于-326年12月19日、终于-325年12月7日;鲁历的N-325始于-326年12月20日、终于-325年12月8日;冬至版夏历的N-325始于-325年2月16日、终于-324年3月5日;颛顼历的N-325始于-326年11月20日、终于-325年11月8日。同样道理,Sy在各历也指不同的时段。
例一: 计算周历在N-386(周元安王十五年)的月份编排。
根据公式(4)和表二,周历最接近-386年1月1日的冬至儒略日数是
JD(W(-386))=1721050.5 + 3/4 - 386×(365 + 1/4) = 1580064.5 + 1/4
冬至日正午的儒略日数是1580065,用儒略日转公历的标准方法(例如理查斯算法)算出儒略日1580065对应的公历日期是-387年12月25日,故周历的冬至在12月25日子正后1/4日(即6时)。用干支网页的公式求得冬至日的天干数是 [下面的mod(X,Y)指X除以Y后所得之余数]
1 + mod(1580065-1, 10) = 5,日天干是戊;冬至日的地支数是
1 + mod(1580065+1, 12) = 3,日地支是寅,所以冬至日干支是戊寅。
周历的正月是建子,也就是说正月含冬至,正月朔是冬至日之前的第一个朔日。用公 式(1)和表二,我们要求出最大的整数i使得
1683430.5 + i·PL < 1580065.5 ⇒ i=floor(-103365/PL) = -3501。
这里floor(x)表示不大于x的最大整数。注意1580065.5是冬至日下一日子正的儒略日数,这是说合朔时刻可以迟于冬至时刻,但不可以迟于冬至所在之日注四,如果-103365/PL是整数的话要减一,因为正月朔不可在冬至下一日的夜半,下一节会介绍一个方法使这特殊情况不会出现。求得i后,合朔的儒略日数是
JD1=1683430.5-3501×(29+499/940)=1580042.5 + 461/940。用上面所述的儒略日转公历和日干支计算算出1580043对应的公历日期是-387年12月3日、日干支是丙辰,这就是周历在N-386的正月初一。合朔离子正有461/940日(今天会说11时46分13秒)。古代计算不用十进制小数,日的小数部分(奇零)以分数表示称为小余,所以461/940是正月朔的小余。
要知道N-386有没有闰月,就要计算正月与下一个正月之间的月数。下一岁的冬至是
JD(W(-385)) = JD(W(-386)) + 365 + 1/4 = 1580430
W(-385)发生在正午,下一日子正的儒略日数是1580430.5。如果N-386没有闰月,N-385正月朔在JD1以后12个朔策;如果N-386有闰月,N-385正月朔在JD1以后13个朔策。
JD1 + 13PL = 1580426.5 + 368/940 < 1580430.5
由此可知N-385的正月在N-386正月的十三个月后,因此N-386有闰月。如果用固定冬至法,闰月置于年终;用无中气法就要找出哪一个月不含中气。中气的儒略日期可用公式(5)计算,即把JD(W(-386)) 累加Ps/12,周历每月的合朔用JD1累加PL便可得,下表给出计算结果。
| JD(朔日)-1580000.5 | JD(中气)-1580000.5 |
|---|---|
| 42 (正月朔) | |
| 64 (冬至) | |
| 72 | |
| 94 (大寒) | |
| 101 | |
| 125 (雨水) | |
| 131 | |
| 155 (春分) | |
| 160 | |
| 186 (谷雨) | |
| 190 | |
| 216 (小满) | |
| 219 | |
| 246 (夏至) | |
| 249 | |
| 277 (大暑) | |
| 278 | |
| 307 (处暑) | |
| 308 | |
| 337 | |
| 338 (秋分) | |
| 367 | |
| 368 (霜降) | |
| 396 | |
| 399 (小雪) | |
| 426 (正月朔) | |
| 429 (冬至) |
JD(朔日)指合朔当日子正的儒略日数,JD(中气)指中气当日子正的 儒略日数,所以减去1580000.5后是整数。表中可见JD(朔日)-1580000.5=308对应的月份不含中气,那是正月之后的第九个朔,所以是闰九月。下表把周历N-386的月份列出。固定冬至法和无中气法所得的朔日完全相同,只是月序不同而已。
| 月序(定冬) | 月序(无中) | 日数 | 朔日干支(公历日期) | 合朔小余 |
|---|---|---|---|---|
| 正 月 | 正 月 | 30 | 丙辰(-387年12月3日) | 461 |
| 二 月 | 二 月 | 29 | 丙戌(-386年1月2日) | 20 |
| 三 月 | 三 月 | 30 | 乙卯(1月31日) | 519 |
| 四 月 | 四 月 | 29 | 乙酉(3月2日) | 78 |
| 五 月 | 五 月 | 30 | 甲寅(3月31日) | 577 |
| 六 月 | 六 月 | 29 | 甲申(4月30日) | 136 |
| 七 月 | 七 月 | 30 | 癸丑(5月29日) | 635 |
| 八 月 | 八 月 | 29 | 癸未(6月28日) | 194 |
| 九 月 | 九 月 | 30 | 壬子(7月27日) | 693 |
| 十 月 | 闰 九 月 | 29 | 壬午(8月26日) | 252 |
| 十 一 月 | 十 月 | 30 | 辛亥(9月24日) | 751 |
| 十 二 月 | 十 一 月 | 29 | 辛巳(10月24日) | 310 |
| 闰 月 | 十 二 月 | 30 | 庚戌(11月22日) | 809 |
每月的日数由该月之朔日与下月之朔日相隔的日数而定,相隔29日是小月,相隔30日是大月。如前述,合朔小余是合朔离子正的时间以分数日表示,分母940往往略去。由于朔策是(29+499/940)日,每月的合朔小余是前月的小余加上499,达到或超过940则减去940,合朔小余如果小于441,加了499后仍小于940,则此月是小月,大于或等于441时则是大月。用现在通行的24小时制来说或会较易理解,朔策是29日12小时44分26秒,所以每月的合朔离午夜零时的时间是前月的时间加上12小时44分26秒,达到或超过24时则减去24,合朔时间如果在11:15:34前,加了12小时44分26秒后仍小于24时,则此月是小月,合朔时间如果在11:15:34或之后则是大月。
例二: 计算冬至版夏历在N-386的月份编排。
根据公式(4)和表二,冬至版夏历最接近-386年1月1日的冬至儒略日数是
JD(W(-386))=1721053.5 + 3/4 - 386×(365 + 1/4) = 1580067.5 + 1/4
儒略日1580068对应的公历日期是-387年12月28日,日干支是辛巳。固定冬至法和无中气法都把冬至固定在夏历的十一月,所以十一月朔发生在冬至的下一日子正之前。用公式(1)和表二,我们要要求出最大的整数i使得
1883590.5 + i·PL < 1580068.5 ⇒ i=floor(-303522/PL) = -10279。
由此可算出十一月朔的儒略日数是
JD1 = 1883590.5 - 10279PL = 1580042.5 + 359/940
合朔小余是359/940。儒略日数1580043对应得公历日期是-387年12月3日,日干支是丙辰。要知道S-386有没有闰月,可以比较儒略日数floor(JD(W(-385))+1.5)和floor(JD1+13PL+0.5)哪个较大。加上0.5是为了使子正的数字由0.5结尾化为整数。
floor(JD(W(-385))+1.5) = floor(1580067.75+365.25+1.5)=1580434,
floor(JD1+13PL+0.5)=floor(1580042.5 + 359/940 + 13×(29 + 499/940) + 0.5) = 1580427 < 1580434
所以S-386是闰岁。固定冬至法规定闰月置于年终,即十二月后,所以正月朔是十一月朔后的第三个合朔,由于这个朔日最接近公历-386年1月1日,根据定义此朔日是夏历N-386的正月朔,前月的闰月属于N-387,因此N-386没有闰月。这是固定冬至法的结果,无中气法则不同,我们要找出此闰岁的无中气月,这可用例一的方法计算,结果是无中气之月在N-387十一月之后的第五个月,属于N-386,因此N-387没有闰月,N-386的正月朔是N-387十一月朔之后的第二个朔,而闰月是N-386的闰三月。下表总结计算结果。
| 月序(定冬) | 月序(无中) | 日数 | 朔日干支(公历日期) | 合朔小余 |
|---|---|---|---|---|
| 闰 月* | 正 月 | 29 | 乙卯(-386年1月31日) | 417 |
| 正 月 | 二 月 | 30 | 甲申(3月1日) | 916 |
| 二 月 | 三 月 | 30 | 甲寅(3月31日) | 475 |
| 三 月 | 闰 三 月 | 29 | 甲申(4月30日) | 34 |
| 四 月 | 四 月 | 30 | 癸丑(5月29日) | 533 |
| 五 月 | 五 月 | 29 | 癸未(6月28日) | 92 |
| 六 月 | 六 月 | 30 | 壬子(7月27日) | 591 |
| 七 月 | 七 月 | 29 | 壬午(8月26日) | 150 |
| 八 月 | 八 月 | 30 | 辛亥(9月24日) | 649 |
| 九 月 | 九 月 | 29 | 辛巳(10月24日) | 208 |
| 十 月 | 十 月 | 30 | 庚戌(11月22日) | 707 |
| 十 一 月 | 十 一 月 | 29 | 庚辰(12月22日) | 266 |
| 十 二 月 | 十 二 月 | 30 | 己酉(-385年1月20日) | 765 |
* 这是N-387的闰月
上节展示的古六历算例用分数处理日的小数部分,主要是为了方便介绍小余这个在书籍和文献常会提及的术语。现代的历法计算多用电子计算机,在计算上分数其实是较为快捷的,在编写计算机程式上处理分数运算却较为费时,所以本网站的历法计算全部不用分数,而是用计算机的浮点运算处理十进位小数。四分术的岁实日数用365.25表示、朔策日数用29.53085106382979表示。但是有一点要注意:当合朔或节气小余是0时,合朔或节气发生在夜半,儒略日数的小数部分是0.5,但是计算机的浮点舍入误差或会使儒略日数的小数部分变成0.49999999999,这会使日期计算有一日之差。为了避免这误差,我把表二的儒略日数加上0.0001。合朔小余总是1/940的整数倍,加了0.0001后,小余的数值变成在0.094/940和939.094/940之间;节气小余总是1/96的整数倍,加了0.0001后,小余的数值变成在0.0096/96 和95.0096/96之间。由於小余不可能是0,浮点舍入误差便不会使日期有偏差了。这方法也使上一节所说的合朔可能出现在子正的特殊情况不会出现,简化计算机程式。
用十进制小数计算时刻,不再须要理会小余,但是如果要计算也可以:
小余 = JD + 0.5 - floor(JD + 0.5) - 0.0001,最后的0.0001是把加上JD的0.0001减去。这小余以十进制小数表示,如果知道小余是1/940的整数倍,要化成以分母为940的分数也可以:
小余 × 940 = floor(940 ( JD + 0.5 - floor(JD + 0.5) )
由于JD加上了0.0001,940 ( JD + 0.5 - floor(JD + 0.5)是某整数加上0.094,floor()则把小数部分删除。
要计算某二十四节气的月龄也很容易,假设JD是某节气的儒略日数,
L = (JD - JD(M0))/29.53085106382979
节气月龄 = L - floor(L)
式中JD(M0)可从表二查得,由于JD和JD(M0)都加了0.0001,相减后不用修正。L是从历元合朔M0起算到该节气的时间间隔以朔策为单位,月龄是节气与上一个合朔的时间间隔,如果以朔策为单位,就是L的小数部分,如果L是负数则须用一减去小数部分。由于floor(L)是不小于L的最大整数,所以上面公式也适用于负数的L,编写程式时无须特别处理。
备 注 和 参 考 文 献
[注一] 古六历的历法假设某节气与合朔发生在同一时刻,在今天来看十分奇怪,因为我们现在知道回归年与朔望月的周期不能约化成简单分数,节气和合朔基本上不可能发生在同一时刻,四分术的235:19比例只是近似值。古人当然不知道,而且古时对冬至的概念没有现代那样有严格的定义,只是以正午时日影最长的那一天为冬至日。即使有了严格定义也没有用,古时的观测较为粗陋,对冬至或合朔的测量或许只准到一日左右,只是在日食发生时,合朔时刻的测定才较为准确。当然,我们可以把「节气合朔齐同」理解为节气与合朔之间的时间相差小于一日左右。编算历法时假设两者时刻相等,可能是为了计算方便,更可能是受到天命论的政治思想影响。不管怎样,以当时的观测精度根本无法判断历法的气朔齐同假设是不是准确。到了后来,观测技术不断提高,那就另当别论了。
[注二] 实际合朔时刻用现代天文的计算方法,即这pdf文件所述的方法,但是岁差要用该文7.2节所说的Vondrák等人的岁差模型计算,算出的TDB时刻用该文第8节的方法转化为世界时UT1时刻。历法合朔时刻用上面公式(1)计算JD(Mi),这可视为是当地的地方时,必须要转化为UT1以和实际合朔的UT1时刻比较。东周的国都是洛阳,其经度是东经112.45°,比UT1迟(112.45/360)日,所以要把算得之JD(Mi)减去(112.45/360)转换成UT1时刻的儒略日。鲁历在鲁国使用,京城是现在的山东省曲阜市,其经度是东经116.98°,儒略日要减去(116.98/360)。颛顼历据说在战国后期在秦国使用,秦国京城咸阳的经度大约是108.9°(用现在西安市的经度)。据说魏国用夏历,魏国的都城大粱接近今天的河南省开封市,经度大约是东经114°。我不知道殷历和黄帝历在哪些诸侯国使用,经度都用东经114°。其实战国时各国的地方时差异小于一小时,即使用其他经度得出的结果也差异甚微。
[注三] 张培瑜在《中国先秦史历表》、《三千五百年历日天象》和《中国古代历法》第三章都说殷历以建子为年首,和一般的说法不同,却没有解释为什么持这不同说法。
[注四] 如果用闰余法,就要改为冬至时刻1580064.5 + 1/4 = 1580064.75:
1683430.5 + i·PL ≤ 1580064.75
注意小于(<)须改为小于或等于(≤),因为可以出现冬至和合朔齐同。[张培瑜87] 张培瑜,《中国先秦史历表》,齐鲁书社(济南),1987年6月。
[张培瑜97] 张培瑜,《三千五百年历日天象》,大象出版社,1997年7月。
[张陈薄胡] 张培瑜、陈美东、薄树人和胡铁珠,《中国古代历法》,中国科学出版社(北京),2008年3月。