六 十 干 支
初稿: 2018年10月 最近一次重大修订: 2019年7月7日
干支是中国传统的纪数系统,现在还在使用。干支纪数是由天干和地支组合。天干有十个,地支有十二个,每一个地支有一种动物与之对应,称为生肖或属相。下表列出所有天干、地支及其对应的十二生肖。
| 天干 | 地支 | 生肖 | ||
|---|---|---|---|---|
| 1 | 甲 | 1 | 子 | 鼠 |
| 2 | 乙 | 2 | 丑 | 牛 |
| 3 | 丙 | 3 | 寅 | 虎 |
| 4 | 丁 | 4 | 卯 | 兔 |
| 5 | 戊 | 5 | 辰 | 龙 |
| 6 | 己 | 6 | 巳 | 蛇 |
| 7 | 庚 | 7 | 午 | 马 |
| 8 | 辛 | 8 | 未 | 羊 |
| 9 | 壬 | 9 | 申 | 猴 |
| 10 | 癸 | 10 | 酉 | 鸡 |
| 11 | 戌 | 狗 | ||
| 12 | 亥 | 猪 | ||
干支纪数由甲子(1,1)起,然后是乙丑(2,2)、丙寅(3,3)、丁卯(4,4)……癸酉(10,10)。到癸酉时天干用尽了,之后的规则是凡是天干或地支用尽后须从头数起,所以癸酉之后是甲戌(1,11)、乙亥(2,12)、丙子等等直到癸亥(10,12)。癸亥后的干支是甲子(1,1),然后是乙丑(2,2)等等循环不息。如下表所示,从甲子到癸亥一共有六十个干支。
| 1 | 甲子 | 16 | 己卯 | 31 | 甲午 | 46 | 己酉 |
| 2 | 乙丑 | 17 | 庚辰 | 32 | 乙未 | 47 | 庚戌 |
| 3 | 丙寅 | 18 | 辛巳 | 33 | 丙申 | 48 | 辛亥 |
| 4 | 丁卯 | 19 | 壬午 | 34 | 丁酉 | 49 | 壬子 |
| 5 | 戊辰 | 20 | 癸未 | 35 | 戊戌 | 50 | 癸丑 |
| 6 | 己巳 | 21 | 甲申 | 36 | 己亥 | 51 | 甲寅 |
| 7 | 庚午 | 22 | 乙酉 | 37 | 庚子 | 52 | 乙卯 |
| 8 | 辛未 | 23 | 丙戌 | 38 | 辛丑 | 53 | 丙辰 |
| 9 | 壬申 | 24 | 丁亥 | 39 | 壬寅 | 54 | 丁巳 |
| 10 | 癸酉 | 25 | 戊子 | 40 | 癸卯 | 55 | 戊午 |
| 11 | 甲戌 | 26 | 己丑 | 41 | 甲辰 | 56 | 己未 |
| 12 | 乙亥 | 27 | 庚寅 | 42 | 乙巳 | 57 | 庚申 |
| 13 | 丙子 | 28 | 辛卯 | 43 | 丙午 | 58 | 辛酉 |
| 14 | 丁丑 | 29 | 壬辰 | 44 | 丁未 | 59 | 壬戌 |
| 15 | 戊寅 | 30 | 癸巳 | 45 | 戊申 | 60 | 癸亥 |
由于干支数是循环的,表一和表二并非显示干支的最好方法,较好的方法是将天干和地支排列在圆环之上:
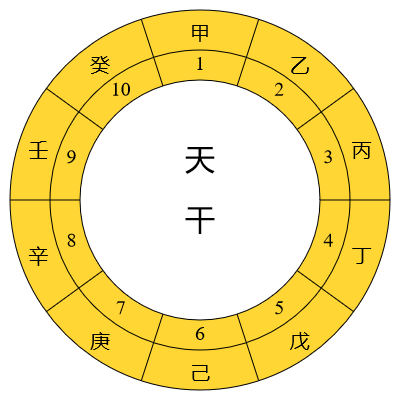
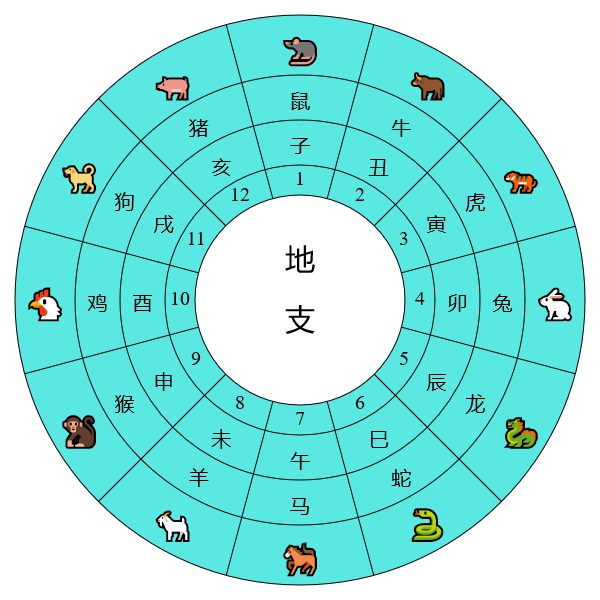
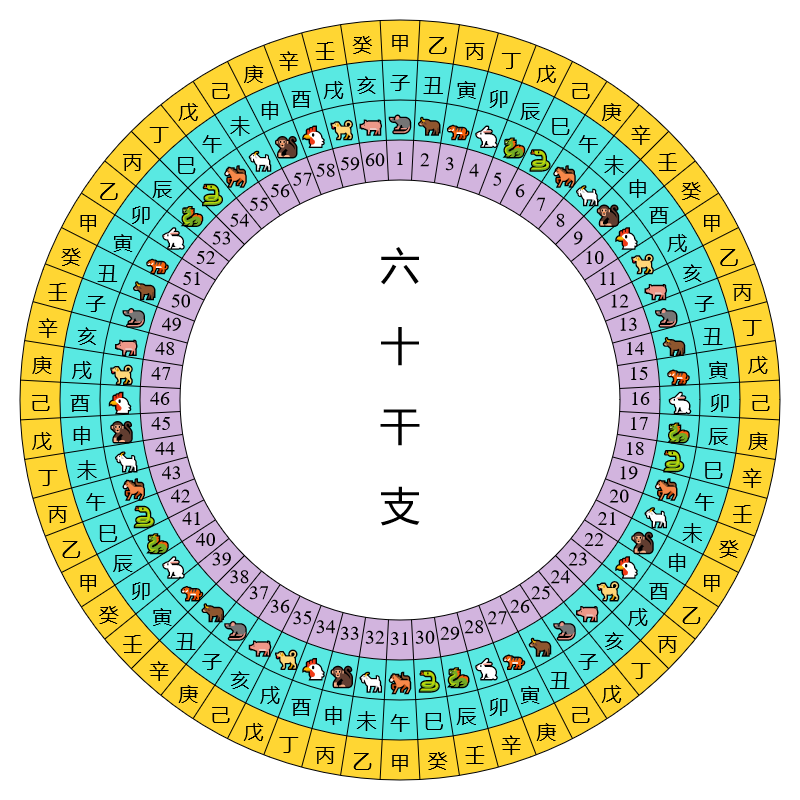
从这些图可见每一个天干、地支和干支组合地位平等,现在天干、地支和干支的数序只是根据传统的习惯来定而已。
干支可用来纪年、纪月、纪日和纪时,但是现在已很少用干支来纪月、纪日和纪时了。下面简略介绍如何用干支来纪年、纪月、纪日和纪时。
干 支 纪 年
现在的农历年一般只用干支纪年,六十年循环一周。最近一周始于1984年农历甲子年。其他公历y年的农历年干支可用同余算术算出。所谓公历y年的农历年是指年首最接近公历y年1月1日的农历年。例如2018年的农历年是指农历戊戌年,始于公历2018年2月16日,终于2019年2月4日。
农历年的天干十年循环一周,年地支十二年循环一周。已知1984年的农历年干支为甲子,以mod(X,Y)表示X除以Y后所得之余数,可推出公历y年之农历年天干数为 1 + mod(y+6, 10),即将公历年数加六,除以十,然后把所得的余数加一。年地支数为 1 + mod(y+8, 12)。依此可算出2018年之农历年天干数为五,即戊,地支数为十一,即戌。所以2018年之农历年干支是戊戌。
月 建 和 「三 正」
月建是指农历月的地支名,但不计闰月,闰月没有月建。由于一年有十二个月(不计闰月),每一个月有固定的月建。建子月取含冬至的月份,建丑月是下一个月(不计闰月),余类推。月建在早期历法颇为重要。
传说早期各朝代以不同的月建作为一年的年首。据说夏代以建寅(即现在的正月)的月份为第一个月;商朝以建丑(即现在的十二月)为第一个月;周朝以建子的月份(现在的十一月)为第一个月。每次更改月份次序,就把更改后的第一个月称为「正月」,「正」是改正的意思。所以夏正为建寅,殷正为建丑,周正为建子。夏正、殷正和周正称为「三正」。
现在一般认为三正之传说不可信。战国时代,各国施行不同历法,当时通行的历法主要有六种:周历、鲁历、殷历、夏历、黄帝历和颛顼历,合称「古六历」。六历之名并非是不同时期不同朝代所制定,而是战国时期的历法家托古而作。所谓「三正」,只是指夏历、殷历和周历所用的三个不同年首。所以「三正」不是夏商周三朝交替使用的历法年首,而是春秋战国时期不同地域施行历法的三个不同年首。
秦朝的历法和颛顼历很接近,两者都是以建亥(现在的十月)作为一年之始,但仍依夏历称建亥为十月,历法的月序是十月、十一月、十二月、正月、二月……九月。汉朝建立后基本上沿用秦历,直到汉武帝太初元年(公元前104年)才颁行新历法,以建寅(正月)为年首。此后二千多年来,除了王莽和魏明帝一度改用殷正,武则天和唐肃宗一度改用周正外,一般都用夏正,到现在仍通行。
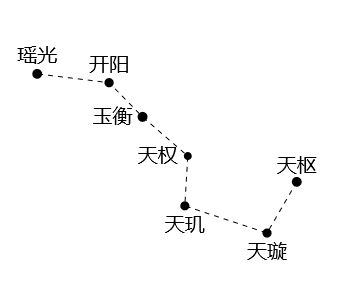
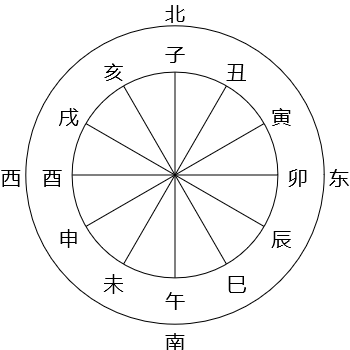
最后要指出,「建」是指北斗七星的斗柄,即玉衡、开阳和瑶光三星(见图一)。方位可用十二地支表示,方法是将地平圈分为十二等分来配十二地支,北方是子,东方是卯,南方是午,西方是酉(见图二)。在古代,北斗七星比现在更接近北天极,在中原地区(约北纬35°)大约在唐朝以前斗柄全年都在地平线之上,那时冬至傍晚可见斗柄指向北(子),所以含冬至的月份称为建子。由于岁差的原故,现在北斗七星离北天极较远。在中原地区,冬至傍晚瑶光在地平线以下,玉衡和开阳在北方地平线附近。现在要去到北纬41°以北的地方才可看到斗柄北指。北纬41°大概在现在的内蒙古呼和浩特市、河北省承德市、辽宁省锦州市等地区。
干 支 纪 月
干支纪月较为复杂,据维基百科所述,有两种干支纪月法。我在年历网页里使用了第一种纪月法。其实干支纪月即使在古代的史书和日历里也不常用,干支纪月最常用于占卜和风水。年历网页里自汉武帝太初元年(公元前104年)起才注有月干支。这里姑且也简单介绍两种干支纪月法。
第一种纪法
此一纪法以农历月配干支,但不计闰月,闰月的干支取上一月的干支。纪法是把月建配上天干,六十月(即五年)循环一周。由于年天干的周期是十年,年干与月干有二对一的对应关系。例如年干为甲或己时,正月的干支必然是丙寅,二月是丁卯,其余可以类推。下表列出月干支与年天干的关系。
| 年天干 | 正月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 | 八月 | 九月 | 十月 | 十一月 | 十二月 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 甲、己 | 丙寅 | 丁卯 | 戊辰 | 己巳 | 庚午 | 辛未 | 壬申 | 癸酉 | 甲戌 | 乙亥 | 丙子 | 丁丑 |
| 乙、庚 | 戊寅 | 己卯 | 庚辰 | 辛巳 | 壬午 | 癸未 | 甲申 | 乙酉 | 丙戌 | 丁亥 | 戊子 | 己丑 |
| 丙、辛 | 庚寅 | 辛卯 | 壬辰 | 癸巳 | 甲午 | 乙未 | 丙申 | 丁酉 | 戊戌 | 己亥 | 庚子 | 辛丑 |
| 丁、壬 | 壬寅 | 癸卯 | 甲辰 | 乙巳 | 丙午 | 丁未 | 戊申 | 己酉 | 庚戌 | 辛亥 | 壬子 | 癸丑 |
| 戊、癸 | 甲寅 | 乙卯 | 丙辰 | 丁巳 | 戊午 | 己未 | 庚申 | 辛酉 | 壬戌 | 癸亥 | 甲子 | 乙丑 |
从上表可方便算出任何农历年的月干支。例如2018年是农历戊戌年,从上表可知年天干为戊的五月干支是戊午,所以戊戌年的五月干支是戊午。有《五虎遁月歌》歌诀以便记忆正(寅)月的月干与年干的关系: 甲己之年丙作初,乙庚之岁戊为头,丙辛岁首从庚起,丁壬壬位顺流行,若问戊癸何方法,甲寅之上好推求。
其实要算出某年的月干只需记住年干为甲时正月的月干是丙就可以了,其他月的月干可先计算其与甲年干的月数,然后用同余算术推出其月干。这里以戊戌年五月为例,戊是甲之后的四个天干,所以如果以甲年算起,戊年五月就是甲年的 (4×12+5) 或五十三月,戊年五月的天干是丙往下数第五十二个天干,由于mod(52, 10) = 2,即五十二除以十之余数为二,丙以后的第二个天干是戊,所以戊戌年的五月的干支是戊午。
这种纪法为明朝和清朝钦天监编的官方历书所采用(见存世明清历书,例如明嘉靖三年大统历、清康熙九年时宪历等),也用于近代历书(例如《100年袖珍干支月历》,刘宝琳(紫金山天文台研究员)编,商务印书馆(香港), 1993)。如上述,闰月没有月建,据明清的历书所载,闰月的月干支以月内之节气划分,节气之前用前月的干支,节气之后用下月的干支。例如清康熙九年闰二月,月内有节气清分在闰二月十五,清明前用正月干支(己卯),清明后用三月干支(庚辰)。
第二种纪法
这种纪法不依农历的月份,而是根据二十四节气分月。子月定为由大雪至小寒前一日,丑月定为由小寒至立春前一日等等。下表列出各月对应的节气段,近似农历月份,和近似的公历日期。
| 月地支 | 节气段 | 近似农历月份 | 近似公历日期 |
|---|---|---|---|
| 子 | 大雪至小寒前一日 | 十一月 | 12月7日–1月5日 |
| 丑 | 小寒至立春前一日 | 十二月 | 1月6日–2月3日 |
| 寅 | 立春至惊蛰前一日 | 正月 | 2月4日–3月5日 |
| 卯 | 惊蛰至清明前一日 | 二月 | 3月6日–4月4日 |
| 辰 | 清明至立夏前一日 | 三月 | 4月5日–5月5日 |
| 巳 | 立夏至芒种前一日 | 四月 | 5月6日–6月5日 |
| 午 | 芒种至小暑前一日 | 五月 | 6月6日–7月6日 |
| 未 | 小暑至立秋前一日 | 六月 | 7月7日–8月7日 |
| 申 | 立秋至白露前一日 | 七月 | 8月8日–9月7日 |
| 酉 | 白露至寒露前一日 | 八月 | 9月8日–10月7日 |
| 戌 | 寒露至立冬前一日 | 九月 | 10月8日–11月6日 |
| 亥 | 立冬至大雪前一日 | 十月 | 11月7日–12月6日 |
二十四节气是根据太阳在天球上的位置而定,不考虑月相,所以是纯阳历。公历也是纯阳历,所以以上各月的公历日期每年最多只有一两日之差。农历是阴阳历,既考虑月相也顾及太阳位置,以上各月的起始日期在农历中可以有多至三十日的变动。
古代称由冬至到下一个冬至的周期为岁,称由农年正月初一到下一年正月初一的周期为年。所以岁是纯阳历的概念,而年则属阴阳历。一岁的周期是三百六十五或三百六十六日,平均值接近回归年(365.242日)。一年的周期大约是三百五十四日(无闰月时)或约三百八十四日(有闰月时)。用这种节气定月的法则,一岁有十二个月,每月大至有三十或三十一日,没有闰月。月份配上天干,六十月(即五岁)循环一周。
干 支 纪 日
日干支以六十天循环一周。中国最迟从春秋鲁隐公三年(公元前720年)起就有史藉用干支纪日,距今已有二千七百多年,其间干支纪日既没有间断,又没有发生过错乱。
日的干支可从该日的儒略日数以同余算术推出。儒略日数是指从公元前4713年1月1日正午起算的积日,所以每日正午的儒略日数是整数。这里没有说明所用的时间标准(UT1 或地方时等),是假设了起算时刻(公元前4713年1月1日正午)和每日正午所指的时刻用相同的时间标准。公历某月日的儒略日数有公式计算(例如维基百科),我也建立了儒略日数和日干支计算器网页,提供公历日期与儒略日数和日干支的转换。
由于日干支的周期是六十天,只要知道某一儒略日数的日干支,便可用同余算术推出儒略日数和日干支的关系。查2019年历,得知公元2019年1月27日的日干支是甲子,而该日正午的儒略日数是2458511。从mod(2458511, 60) = 11,可推出某日正午儒略日数JD正午与日干支的关系是
日干支数 S=1+mod(JD正午-11, 60)。 (1)
此处干支数是指按上面表二所列的干支次序,即1代表甲子、2代表乙丑、3代表丙寅等等。若以T代表天干数及B代表地支数,即T和B是上面表一列出的天干和地支次序,则知道了S后便可用以下公式计算天干数和地支数:
T=1+mod(S-1, 10), B=1+mod(S-1, 12)。 (2)
干支数S虽然在古代历法计算中有时有用,但我认为在大多数情况下是不必要的。天干数T和地支数B可以直接用JD正午计算。这可从日天干的周期是十天、日地支周期是十二天、以及上述JD正午=2458511对应的日干支是甲子(T=1、B=1)推出。从mod(2458511, 10) = 1及mod(2458511, 12) = 11得出以下公式:
T=1+mod(JD正午-1,10), B=1+mod(JD正午+1,12)。 (3)
这公式甚为方便,尤其是我们用十进制,天干数T根本不用计算。T基本上就是JD正午的最后一个数位的数,唯一例外是如果该数是0,则T是10。现在看一算例:公元1781年3月13日正午的儒略日数是2371629,因此T=9,天干是壬;B=1+mod(2371630,12)=11,地支是戌,所以日干支是壬戌。
顺带一提,用JD正午也很容易计算星期。星期的周期是七天,已知2019年1月27日是星期日、JD正午=2458511、mod(2458511, 7)=6,由此可推出星期数W和JD正午的关系如下:
W = mod(JD正午+1, 7) (4)
星期数W=0代表星期日、W=1代表星期一、W=2代表星期二等等。年历网页的星期就是用公式(4)计算。
又顺带一提,知道了干支数S后,天干数T和地支数B可用公式(2)轻易计算。反过来,知道天干数T和地支数B后,要求干支数S就要解以下的同余方程:
S ≡ T (mod 10), S ≡ B (mod 12)。
此处≡符号表示同余。上面公式是说S-T可被10整除、S-B可被12整除。如果不熟悉同余算术,要找出一条算式来表示S也许会有点困难。对于某一特定的T和B,当然可以查表二找到答案。如果认为查表二等于「作弊」,可以用以下公式计算:
先算 k=6T-5B,如果k>0,则 S=k; 如果k≤0,则 S=k+60。也可以证明k>0等同于T≥B,k≤0等同于T<B,而T-B必定是偶数。[1]
以上面算出的壬戌干支为例,T=9、B=11,k=6×9-5×11=-1,所以S=59,正是表二列出壬戌的干支次序。
以上所述的同余算术问题并不难。我没有正式学过同余算术理论,但仍能輕易求出其解,原因是求解过程中不须要用到如大衍求一术这样精妙的算法[2]。稍为艰难的算题见于《孙子算经》,即著明的「物不知数」算题:[3]「今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?」用现代数学算式表示,就是要求一整数x,使得
x ≡ 2 (mod 3), x ≡ 3 (mod 5), x ≡ 2 (mod 7)。
中国古代学者在计算历法时遇到了不少同余算术问题(尤其是计算上元积年),很可能因此深入研究同余算术,发现了著明的孙子定理,西方称为「中国剩余定理」。
干 支 纪 时
古时将一日分为十二时辰。用现在通用的时间系统来说,一时辰相当于现在的二小时。十二时辰正好配十二地支,所以时辰一般只提地支,不理天干。以现时通用的时间系统来说,子时是晚上十一时至凌晨一时,丑时是凌晨一时至三时,其余可以类推。
十二时辰配上天干后,就有六十时辰(即五日)的周期。日干的周期是十日,所以日干与时干有二对一的对应关系,颇似年干与月干的关系。日干与时干也有类似的对照表,但我认为只须知道日干为甲的子时天干是甲就可以了,其他时干可用同余算术推出。这里以丁日的未时为例,丁是甲之后的第三个天干,未是第八个地支,丁日的未时即从甲日算起的第(3×12 + 8)个时辰,即第四十四个时辰,所以其天干是从甲起往下数四十三个天干,四十三除以十余数是三,甲之后第三个天干是丁,所以丁日未时的时辰干支是丁未。
备 注
[1] 要验证S的公式确能满足方程(2)不难。首先是把S的公式写成:
S = 6T - 5B + 60n,如果T≥B,则n=0;如果T<B,则n=1。
由于T和B之差必是偶数,可把B写成B=T+2j,这里j是某整数,把此式代入S的公式便得:
S = T - 10j + 60n。由于10j和60n都可被10整除,所以
mod(S-1, 10) = mod(T-1, 10) = T-1。
这公式符合方程(2)的左边公式。最后一个等式成立是因为T-1是0和9之间的整数。
用T=B-2j代入S的公式得出
S = B - 12j + 60n。由于12j和60n都可被12整除,所以
mod(S-1, 12) = mod(B-1, 12) = B-1,符合方程(2)的右边公式。
[2] 我的推导方法是把S的同余方程写成以下公式:
S=T+10i, S = B+12j, i和j是某整数。
⇒ T+10i = B+12 j
⇒ 6j-5i = (T-B)/2.
i=j=(T-B)/2显然是一解,所以
S = T+10i = T+5(T-B) = 6T-5B,但当T<B时,此数是负数或0,所以此时要加上60使S规范在1和60之间。
这推导中最关键的一步是求两整数p和q满足方程6p-5q=1。求得p和q后,乘(T-B)/2就得i和j。这方程相当简单,p=q=1明显是一解。如果要解的方程是aj-bi=1而a和b是其他整数,或许不会那么容易猜到答案,那时就要用大衍求一术求解。
[3] 此算题相当著明,甚至连金庸武侠小说《射雕英雄传》也引用。书中说郭靖和黄蓉离开瑛姑居所前,黄蓉出了三道算题考瑛姑,第三道题就是物不知数算题。后来黄蓉与瑛姑再碰面,问起那三道算题,瑛姑却一道题也算不出,她对物不知数算题尤其感兴趣:「这第三道题呢,说易是十分容易,说难却又难到了极处……我知道这(答案)是二十三,不过那是硬凑出来的,要列一个每数皆可通用的算式,却是想破了脑袋也想不出。」黄蓉于是说出答案:「以三三数之,余数乘以七十;五五数之,余数乘以二十一;七七数之,余数乘十五。三者相加,如不大于一百零五,即为答数;否则须减去一百零五或其倍数。」
用现代数学的数式表示或会有助理解。用a、b、c表示未知数x被三、五、七除后所得之余数,《孙子算经》给出的答案是
x = 70a + 21b + 15c - 105n,n是任意整数。
推导此式须要用孙子定理,一般谈论同余算术的书藉或文章应该有论述(例如这篇文章)。但是要验证这答案确能满足算题的要求却不难:由于21b、15c和105n都可被三整除,mod(x,3) = mod(70a, 3) = mod(3×23a+a,3) = mod(a,3)=a,用类此计算可得mod(x,5)=b及mod(x,7)=c。