Reconstruction of Calendars in the Qin and Early Han Dynasties (221 BCE – 104 BCE)
First draft: April, 2019
On this webpage, I describe the method used to reconstruct the calendar used in the Qin and Early Han dynasties, covering the period from 221 BCE to 104 BCE. The reconstruction method is claimed to be valid from 246 BCE to 104 BCE, but we only use it for the period from 221 BCE to 104 BCE. The reconstruction method is based on the paper "Researches on Calendars from Qin to early Han (246 B.C. to 104 B.C.) — centering on excavated calendrical bamboo slips"Li12 by Lǐ Zhōnglín (see also his book On the Calendric System of the Qin and Early Han DynastiesLi16). The gist of the reconstruction method is to divide the time interval between 245 BCE and 104 BCE into three periods. Lunar conjunctions in each period are calculated based on the sìfēn system. The only difference between the three periods is the epoch of the sìfēn system, which can be regarded as a free parameter in the system used to compute the lunar conjunction times. The 24 solar terms are computed in the same way as the Zhuanxu calendar, one of the ancient six calendars. The intercalary (leap) months are inserted following a 3-3-3-2-3-3-2 pattern in a 19-year (zhāng) cycle discussed on our ancient six calendars page. According to Lǐ, this is just an empirical rule used at that time and has nothing to do with the 24 solar terms, a viewpoint not shared by most scholars. I don't fully agree with him either and think the issue requires further study. However, I will not discuss the issue here as it's not directly related to the reconstruction method.
The reconstruction method relies heavily on the sìfēn system, which is discussed in detail on our ancient six calendars page and will not be repeated here.
Contents
- Introduction
- Computation of Solar Terms and Conjunction
- Leap Months and Accumulated Months
- Examples
- Time Lags of the Calendrical Conjunctions
- Table of Solar Terms
The calendrical system used in the Qin and Early Han dynasties (221 BCE – 104 BCE) has been puzzled by scholars in the past centuries. According to Shǐjì (史記 or Records of the Scribe), the calendar used by the early Han dynasty was the same as that of the Qin dynasty (221 BCE – 207 BCE). Hànshū (漢書 or Book of Han) further explains that the calendar used by the Qin dynasty was the Zhuanxu calendar, one of the ancient six calendars believed to have been used in the Warring States period (480 BCE – 222 BCE). However, it has been known for a long time that the dates computed by the Zhuanxu calendar do not agree with the dates appeared in the historical documents. They match more closely with those computed by the Yin calendar, another one of the ancient six calendars. Scholars from the 11th century to 20th century thought that the Qin and Han calendar was either the Zhuanxu calendar or the Yin calendar. However, an archeological discovery in 1972 shattered this view.
**************************
Before I go on, it is useful to introduce a notation to label the years in the Chinese calendar. Even though a Chinese year does not coincide with a year in the Western calendar, it is possible to establish a simple mapping from a Chinese year to a Western year. This is because the Chinese calendar is a luni-solar calendar. The average number of days in the calendar is close to a tropical year. Therefore, there is no secular drift between the years in the Chinese calendar and Western calendar. Hereafter, I use the notation Ny to denote the Chinese year whose New Year day is closest to Jan. 1 of the Western year y. For example, N-100 refers to the Chinese year whose New Year day was closest to Jan. 1, -100 (101 BCE). It turns out the New Year day of N-100 was on Feb. 19, -100 in the proleptic Julian calendar, and the last day of N-100 was on Feb. 7, -99.
**************************
In 1972, bamboo slips were excavated from Yínquèshān (銀雀山) in Shāndōng province in eastern China. The bamboo slips contain a calendar table for the year N-133, providing very valuable information on how months and days were arranged in that year. The calendar table lists the sexagenary names of the first days in each month. The year N-133 had 13 months, with a leap month placed at the end of the year. Of the 13 sexagenary dates for the 13 months, only 7 of them match those calculated by the Zhuanxu calendar and 10 of them match those calculated by the Yin calendar. This means that the calendar used in N-133 was neither the Zhuanxu calendar nor Yin calendar. Historians and astronomers were excited by this discovery and attempted to figure out what system the calendar was based on.
Even though the calendar in N-133 was not one of the ancient six calendars, it is generally believed that the calendar in that period was still based on the sìfēn system. It is also clear from the excavated calendar table, as well as historical documents, that the month order of the calendar at that time was the same as the Zhuanxu calendar, in which the first month of a year began with month 10, followed by month 11, month 12, month 1, ..., month 9. A leap month was placed at the end of a year after month 9 and was called post month 9 (後九月). The problem is that there are many ways to construct a calendar based on the sìfēn system that matches all the data in the excavated calendar table. In Section 3.9 of the book Ancient Chinese Calendars and AlmanacsZCBH08 and in the paper "An Attempt to Discuss the Calendrics of the Qin and Early Han According to Newly Excavated Calendars on Slips and Boards"Zhang07, Zhāng Péiyú states that there are 58 possible ways of reproducing the calendar dates in N-133 based on the sìfēn system. The maximum deviation of the lunar conjunction times between these 58 systems is 87 minutes. Many scholars proposed their own methods of reconstructing the calendar around that period. Without new data, it was impossible to tell which of these methods was correct.
New data did appear thanks to archeological discoveries in the 1980s and early 2000s. More calendrical bamboo slips were excavated from two tombs, covering years from N-201 to N-185, and several years between N-244 and N-208. These new data indicate that the calendar between 245 BCE and 104 BCE was more complicated than previously thought. They suggest that the calendar in the Qin dynasty (before 206 BCE) was based on a different system from the calendar in early Han dynasty around 200 BCE, and the calendar used in N-133 was based on a system different from the other two. None of the previous reconstruction methods proposed to fit the N-133 data matches all the new data.
I know of two papers attempting to find methods to reconstruct the calendar in this period based on all the available datafn1. One is the paper by Zhāng Péiyú in 2007 mentioned aboveZhang07. The other is "Researches on Calendars from Qin to early Han (246 BCE to 104 BCE) — centering on excavated calendrical bamboo slips"Li12 by Lǐ Zhōnglín in 2012. This research has also been incorporated in his book On the Calendric System of the Qin and Early Han DynastiesLi16 published in 2016. I thank Prof. Lǐ Zhōnglín for sending me his book. The proposed reconstruction methods by these two authors are not the same, even though they all fit the available data.
Zhāng proposes two reconstruction methods, one for the calendar in the Qin dynasty (before N-205), and the other for the early Han dynasty until 104 BCE. The method for the Qin calendar is based on the sìfēn system with the epoch at the time when the lunar conjunction and the solar term Z9 were assumed to both occur at midnight on Oct. 27, 607 BCE. Intercalation was determined by the requirement that the solar term Z10 was always in month 10 (solar term labels are given on our solar terms page). The conjunction dates associated with all months in N-245 – N-206 are listed in Table 9 at the end of the paper.
For the early Han calendar, Zhāng concludes that it is impossible to find a calendar based on the sìfēn system that can fit all the data. In other words, if the calendar used in the early Han was based on the sìfēn system, there must be some changes during the period. If there was no change in the calendar, it could not be based on the sìfēn system. Zhāng decides to give up the sìfēn system and finds another system that fits the data. His reconstruction method is to adopt a lunar cycle of (29 + 663/1249) days, and a solar cycle of 365.2496734 days or (365 + 311.8420766/1249) days. The seeming strange number for the solar cycle comes from the 235:19 ratio between the solar and lunar cycles. The solar cycle can also be written as (365 + 5925/23731) days. The 235:19 ratio is chosen to enforce the 19-year (zhāng) cycle. Zhāng does not specify an epoch for the reconstruction method, but he provides the conjunction dates associated with all months in N-205 – N-104 in Table 10 at the end of the paperfn2. The paper doesn't mention what intercalation rule is used. Zhāng mentions an intercalation rule for another reconstruction method (which is inferior since it doesn't match all the data), which is the requirement of the solar term J1 always being in month 1. This is a very strange rule as it clearly doesn't fit the data. I am able to reproduce his Table 10 using the intercalation rule mentioned in Section 3.9 of the book Ancient Chinese Calendars and AlmanacsZCBH08. The rule is to require the winter solstice to be in month 11 for the years before N-162, and to require the solar term Z1 to be in month 1 for the years after N-162.
Zhāng's use of a non-sìfēn system is similar to the method he used to reconstruct the Chunqiu calendar used by the Lu state in the Spring and Autumn period (this website adopts his reconstruction method of the Chunqiu calendar and the method is explained on our Chunqiu calendar page). He doesn't provide any reason as to why this is a good approach. I think it is only a model designed to fit the data, and not likely to be the actual rule used in the early Han period.
Now let's turn to Lǐ Zhōnglín's approach. Since there is evidence to suggest that three different systems were used in the calendar dates on the bamboo slips, the simplest assumption is that the calendrical system was modified at least twice. Lǐ attempts to divide the time interval into three periods and use three different methods based on the sìfēn system to fit the data. He assumes that the 24 solar terms were calculated in the same way as in the Zhuanxu calendar. The only difference between the three methods is the epochs used to compute the lunar conjunctions. He names the epochs simply by A, B and C. Epoch A was at midnight on Nov. 18, 362 BCE. Epoch B was at midnight on Oct. 31, 241 BCE. Epoch C was at midnight on Dec. 14, 207 BCE. In all three cases, lunar conjunctions were assumed to have occurred at these epochs. Epoch A applies to the calendar in the period from circ. N-245 to month 12 in N-201. Epoch B applies to the calendar in the period from month 1 in N-201 to the end of N-163. Epoch C applies to the calendar in the period from N-162 to month 5 in N-103.
Lǐ proposes that the leap months were inserted based on an empirical rule following a 3-3-3-2-3-3-2 pattern in a zhāng cycle. He points out in a paper published in 2009Li09 that all of the leap months between N-245 and N-104 can be deduced by the excavated calendrical bamboo slips and the available historical documents. As a result, it is not necessary to know the actual intercalation rules to reconstruct the calendar in this period. So I will not discuss the highly debated intercalation rules here.
Even though the reconstruction methods proposed by Zhāng and Lǐ are quite different, their discrepancies are quite small. Of the 140+ years between N-245 and N-104, there were 1700+ lunar conjunctions and only 19 mismatches of the dates among these conjunctions between Zhāng's and Lǐ's. The following table lists these 19 mismatches.
| Chinese Year | Chinese Month | Conjunction Day — Zhāng | Conjunction Day — Lǐ* |
|---|---|---|---|
| N-245 | 2 | Wù Shēn (Mar. 5, -245) | Dīng Wèi (Mar. 4, -245) |
| N-239 | 9 | Gēng Zǐ (Sep. 21, -239) | Jǐ Hài (Sep. 20, -239) |
| N-232 | 3 | Rén Chén (Apr. 9, -232) | Xīn Mǎo (Apr. 8, -232) |
| N-226 | post 9 | Jiǎ Shēn (Oct. 27, -226) | Guǐ Wèi (Oct. 26, -226) |
| N-204 | 10 | Xīn Sì (Nov. 3, -205) | Rén Wǔ (Nov. 4, -205) |
| N-204 | 12 | Gēng Chén (Jan. 1, -204) | Xīn Sì (Jan. 2, -204) |
| N-204 | 2 | Jǐ Mǎo (Feb. 29, -204) | Gēng Chén (Mar. 1, -204) |
| N-203 | 2 | Guǐ Mǎo (Mar. 19, -203) | Jiǎ Chén (Mar. 20, -203) |
| N-203 | 4 | Rén Yín (May 17, -203) | Guǐ Mǎo (May 18, -203) |
| N-202 | 7 | Yǐ Chǒu (Aug. 3, -202) | Bǐng Yín (Aug. 4, -202) |
| N-202 | 9 | Jiǎ Zǐ (Oct. 1, -202) | Yǐ Chǒu (Oct. 2, -202) |
| N-183 | 2 | Dīng Chǒu (Mar. 8, -183) | Wù Yín (Mar. 9, -183) |
| N-177 | 9 | Jǐ Sì (Sep. 25, -177) | Gēng Wǔ (Sep. 26, -177) |
| N-170 | 3 | Xīn Yǒu (Apr. 13, -170) | Rén Xū (Apr. 14, -170) |
| N-163 | 10 | Guǐ Chǒu (Oct. 30, -164) | Jiǎ Yín (Oct. 31, -164) |
| N-136 | 5 | Guǐ Mǎo (May 26, -136) | Jiǎ Chén (May 27, -136) |
| N-129 | 11 | Yǐ Wèi (Dec. 13, -130) | Bǐng Shēn (Dec. 14, -130) |
| N-112 | 12 | Bǐng Xū (Ja. 4, -112) | Dīng Hài (Jan. 5, -112) |
| N-106 | 7 | Wù Yín (July 23, -106) | Jǐ Mǎo (July 24, -106) |
* There is a typo in Lǐ's calendar table in N-199: the sexagenary date of the conjunction day in month 5 should be changed from Jǐ Sì to Jǐ Mǎofn3. This typo is corrected in the book On the Calendric System of the Qin and Early Han DynastiesLi16.
Since the reconstructed calendars of Zhāng and Lǐ both fit the available data and their differences are small, one can choose either of them to reconstruct the calendar between N-245 and N-104. The calendar from N-220 (or 221 BCE) to month 4 in N-103 on this website is reconstructed using Lǐ's method. The following sections describe the implementation.
The calculation of solar terms is the same as in the Zhuanxu calendar, which is described on the ancient six calendars page. Here I only list the formulae. According to equation (4) and Table 2 on the ancient six calendars page, the Julian day of the winter solstice closest to year y is given by
JD(W(y)) = 1721050.5 + 19/32 + y·Ps (1)
where Ps = 365.25 is the number of days in a solar cycle in the sìfēn system. The other solar terms can be calculated using equation (5) on the ancient six calendars page:
JDq(j, y) = JD(W(y)) + (j/24)·Ps (2)
Here j is the solar-term number counting from the winter solstice, with j=0 for the winter solstice (Z11), j=1 for J12, j=2 for Z12, j=3 for J1, ..., j=23 for J11. With the exception of the winter solstice being in late December in year y-1, all other 23 solar terms computed using equation (2) are in year y.
The times of lunar conjunctions can be written in the form as in equation (1) on the ancient six calendars page:
JD(Mi) = JD(M0) + i· PL (3)
Here PL = 29 + 499/940 is the number of days in a lunar cycle in the sìfēn system, i is the lunation number from the conjunction M0 at the epoch, and Mi is the ith conjunction after M0.
As stated in Introduction, three epochs are used for the calendar between N-245 and N-104. These epochs are used only for the computation of lunar conjunctions. Take epoch A as an example, which assumes a lunar conjunction occurred at midnight on Nov. 18, 362 BCE in the proleptic Julian calendar, corresponding to a Julian day number of 1589523.5. Hence we have JD(M0) = 1589523.5 for epoch A. Values of JD(M0) for the two epochs can be calculated or looked up from the dates in the proleptic Julian calendar. The following table summarizes the result.
| Epoch A | Epoch B | Epoch C | |
|---|---|---|---|
| Epoch | Nov. 18, 362 BCE | Oct. 31, 241 BCE | Dec. 14, 207 BCE |
| Applicable Period | circ. N-245 – N-201 month 12 | N-201 month 1 – N-163 | N-162 – N-103 month 5 |
| JD(M0) | 1589523.5 | 1633701.5 | 1646163.5 |
If we know the number of lunations A(y) associated with the New Year day conjunction of Ny from the epoch conjunction M0, the New Year day conjunction time can be computed using equation (3) with i replaced by A(y). Having computed the New Year day, the conjunctions associated with the other months in Ny can be computed by adding integer multiples of PL. However, we need to know the leap months before Ny in order to compute the accumulated months A(y). Leap months and calculation of A(y) are discussed in the following section.
As stated in Introduction, all of the leap months between N-245 and N-104 can be deduced from the excavated calendrical bamboo slips and available historical documents. We can therefore use these known leap months to calculate A(y) without relying on any particular intercalation rule. This is the approach adopted here.
The accumulated months A(y) can be calculated in the same way as described in the Chunqiu calendar page. The leap months in the Chunqiu calendar were irregular and so A(y) must be computed year by year based on the leap month information. By contrast, leap months between N-245 and N-104 followed the regular 3-3-3-2-3-3-2 pattern, but the leap-year cycle was interrupted after N-162 and the counting was reset to a different year of origin after that. It is therefore not necessary to calculate A(y) year by year. We only need the data in a zhāng cycle, which can be captured by two functions J and R defined in the following table.
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J(k) | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| R(k) | 0 | 12 | 24 | 37 | 49 | 61 | 74 | 86 | 98 | 111 | 123 | 136 | 148 | 160 | 173 | 185 | 197 | 210 | 222 |
Here k is the number of years from the beginning of a zhāng cycle: k=0 means the first year in the cycle, k=1 the second year, k=2 the third year, ..., k=18 the 19th (last) year. The value of J(k) is an indicator of whether or not the year has a leap month: J(k)=0 means no leap month, J(k)=1 means there is a leap month. The sequence 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1 appearing in J(k) shown in the table is exactly the 3-3-3-2-3-3-2 pattern. The value of R(k) is the total number of months from the first month of a zhāng cycle. It begins with 0 at k=0, and increases by 12 or 13 each year: 12 if there is no leap month and 13 if there is a leap month. Hence, R(k) follows the recurrence formula
R(0) = 0 , R(k)= R(k-1) + 12 + J(k-1) (k = 1, 2, 3, ..., 18) (4)
The values of R(k) in Table 3 are computed from this recurrence formula. Now that we have J and R, A(y) can be computed using the following equations.
c = floor( (y - yz)/19 ) (5)
k = y - yz - 19c (6)
Leap month: No leap month if J(k)=0, a leap month if J(k)=1 (7)
Accumulated months: A(y) = ΔA + 235c + R(k) (8)
Here floor(x) denotes the largest integer smaller than or equal to x, yz is the first year of a particular zhāng cycle. As mentioned above, the leap-year pattern was interrupted in N-162 and the counting was reset to a different yz. Thus there are two different values of yz, one for years before N-162 and the other for years after N-162. The variable c in equation (5) is the number of zhāng cycles between yz and the zhāng cycle the year y was in. The variable k in equation (6) is the number of years between year y and the beginning of its zhāng cycle. It can also be written as k = mod(y - yz, 19), where mod(X,Y) denotes the remainder of X divided by Y. The last two terms in equation (8) is the accumulated number of months between the first month of yz and the first month of Ny, but A(y) is the accumulated months between the epoch conjunction M0 and the first month of Ny. So a correction term ΔA has to be included in equation (8). Values of ΔA and yz for the three epochs are listed in the table below. Information from Table 2 is also listed for convenience. As mentioned above, yz switches from one value to another after N-162, but N-162 is the first year when the epoch is switched to epoch C. So yz is the same for epochs A and B, but changes to a different value for epoch C.
| Epoch A | Epoch B | Epoch C | |
|---|---|---|---|
| Epoch | Nov. 18, 362 BCE | Oct. 31, 241 BCE | Dec. 14, 207 BCE |
| Applicable Period | circ. N-245 – N-201 month 12 | N-201 month 1 – N-163 | N-162 – N-103 month 5 |
| JD(M0) | 1589523.5 | 1633701.5 | 1646163.5 |
| yz | -225 | -225 | -179 |
| ΔA | 1670 | 174 | 321 |
Calendars from N-245 to N-104 can be reconstructed using equations (1)–(3), (5)–(8), and Tables 2–4. Two examples are shown in the next section to demonstrate the calendar calculation.
Even though the reconstruction method is claimed to be valid for calendars from N-245 to month 5 in N-103, our calendar page uses this method from 221 BCE to month 4 in N-103 and our calendar table page uses this method from N-220 to month 4 in N-103 (the calendar page is mainly based on the Western calendar and the calendar table page is mainly based on the Chinese calendar). Starting in month 5 in N-103, both pages use the data from the book 3500 Years of Calendars and Astronomical PhenomenaZhang97, which shows calendar data based on the Tàichū astronomical system (太初曆) beginning in month 1 in N-103fn4. In N-103, month 3 had 29 days and month 4 should have had 30 days according to the reconstructed calendar. However, when the new calendar was used in month 5, the conjunction day moved one day earlier, turning month 4 into a short month. Month 5 was a short month in the new calendar. As a result, months 3, 4, 5 in N-103 all had 29 days. This is impossible for any calendar based on the píngshuò rule (based on the mean motions of the Moon and Sun), and could only occur when switching to a new calendar. If the switch is changed to month 6, month 5 will have 28 days, which is also impossible under normal circumstances.
Example 1: Calculate all months in N-130, the dates and lunation fractions of the solar terms Z10, Z11 (winter solstice) and J1.
Let's first calculate the months. From Table 4, epoch C should be used for N-130, JD(M0) = 1646163.5, yz = -179 and ΔA = 321. It follows from equations (5)–(8) and Table 3 that
c = floor( (-130 + 179)/19) = 2
k = -130 + 179 - 19×2 = 11
J(11) = 0 ⇒ no post month 9 (leap month) in N-130
A(-130) = 321 + 235×2 + 136 = 927.
The Julian day of the month 10 conjunction time in N-130 was
JD10 = 1646163.5 + 927×(29+499/940) = 1673538.5 + 93/940
This means the xiǎoyú of the conjunction was 93 (omitting the denominator 940). In the 24-hour time system used today, this means the conjunction was at 2:22:28. The Julian day number at noon of the conjunction day was 1673539. Using the standard algorithm for converting Julian days to calendar dates (e.g. algorithm by Richards), the Julian day 1673539 corresponds to Nov. 25, 132 BCE in the proleptic Julian calendar. According to the formulae for converting Julian days to sexagenary cycle names on our sexagenary cycle page, the stem number of the sexagenary cycle on the conjunction day was
1 + mod(1673539-1, 10) = 9,and the stem name was rén. The branch number was
1 + mod(1673539+1, 12) = 9,and the branch name was shēn. So the sexagenary date was rén shēn.
The other conjunction times in N-130 can be computed by adding integer multiples of PL. The traditional method is to use fractions to do the calculation. Take month 11 as an example. The month 10 conjunction was on Nov. 25, 132 BCE (sexagenary date rén shēn) and the xiǎoyú was 93. The lunar cycle is (29 + 499/940) days. Adding 499 to 93 yields 592. Since the number is smaller than 940, the month 11 conjunction day was 29 days after the month 10 conjunction day and the xiǎoyú of the month 11 conjunction was 592. Month 11 conjunction occurred on Nov. (25+29) = Dec. (25+29-30) = Dec. 24. The sexagenary date was 29 days after the rén shēn date. 29 = 30-1 = 2×12 + 5, so the stem name was one stem before rén (which was xīn) and the branch name was 5 branches after shēn (which was chǒu). The sexagenary date of month 11 conjunction was xīn chǒu. Of course, using Julian days to do the calculation is easier for implementation on a computer. The following table lists the dates of all months in N-130.
| Chinese month | Conjunction date | xiǎoyú |
| 10 (S) | Nov. 25, 132 BCE (Rén Shēn) | 93 |
| 11 (L) | Dec. 24, 132BCE (Xīn Chǒu) | 592 |
| 12 (S) | Jan. 23, 131BCE (Xīn Wèi) | 151 |
| 1 (L) | Feb. 21 (Gēng Zǐ) | 650 |
| 2 (S) | Mar. 23 (Gēng Wǔ) | 209 |
| 3 (L) | Apr. 21 (Jǐ Hài) | 708 |
| 4 (S) | May 21 (Jǐ Sì) | 267 |
| 5 (L) | June 19 (Wù Xū) | 766 |
| 6 (S) | July 19 (Wù Chén) | 325 |
| 7 (L) | Aug. 17 (Dīng Yǒu) | 824 |
| 8 (S) | Sep. 16 (Dīng Mǎo) | 383 |
| 9 (L) | Oct. 15 (Bǐng Shēn) | 882 |
In the table, L means the month had 30 days and S means the month had 29 days. The number of days in a month is determined by the number of days between two successive conjunction dates. The xiǎoyú of a conjunction is the conjunction time from midnight expressed as a fraction of a day. The denominator 940 is often omitted. Since the lunar cycle is (29 + 499/940) days. The xiǎoyú of a conjunction increases by 499 (mod 940) every month. If the xiǎoyú is smaller than 441, adding 499 to it will still be smaller than 940 and the number of days in the month is 29. If the xiǎoyú is equal to or greater than 441, adding 499 to it will make the conjunction time at or past midnight, and the conjunction will be on the next day. There will be 30 days in the month in this case.
Now we calculate solar terms. Let's start with Z11 (winter solstice). It follows from equation (1) that the Julian day of Z11 in N-130 was
JDZ11 = JD(W(-130)) = 1721050.5 + 19/32 -130×365.25 = 1673568.5 + 3/32.
The xiǎoyú of the winter solstice was 3/32. The Julian day at noon on the solstice day was 1673569. Using the same conversion method as above, I get the Z11 day on Dec. 25, 132 BCE and the sexagenary date was rén yín. We can see from Table 5 that Z11 fell on the second day in month 11 in the Han calendar. As for the lunation fraction of Z11, it was the time difference between Z11 and its previous lunar conjunction expressed as a fraction of a lunar cycle. The lunar conjunction before Z11 was the month 11 conjunction and its Julian day was
JD11 = JD10 + 29 + 499/940 = 1673567.5 + 592/940,
lunation fraction of Z11 = (JDZ11 - JD11)/(29 + 499/940) = 1163/74024 ≈ 0.3/19.
I used fractions in the above calculations for convenience of showing the values of xiǎoyú. All calendar calculations on this website use decimals, which is explained in the last section on the ancient six calendars page. The last formula on that page shows a convenient way of calculating the lunation fraction:
L = (JD - JD(M0))/29.53085106382979 (9)
lunation fraction of a solar term = L - floor(L) (10)
where JD is the Julian day of the solar term and JD(M0) is the Julian day of the lunar conjunction at the epoch given in Table 2. The value of L is the time difference between the solar term and lunar conjunction at the epoch M0 in units of lunar cycles. The lunation fraction of a solar term is the time difference between the solar term and its previous lunar conjunction in units of lunar cycles, which is simply the fractional part of L. Take Z11 in N-130 as an example. We have
L = (JDZ11 - 1646163.5)/29.53085106382979 = 928.0157111207177
lunation fraction of Z11 = L - floor(L) = 0.01571112207177 ≈ 0.3/19,
which agrees with the calculation above. Since the Julian day of a lunar conjunction is an integer multiples of lunar cycles plus JD(M0), we can use the Julian day of any conjunction to calculate L. We get a different integer part but the fractional part remains unchanged. Take JD10 as an example, we have
L = (JDZ11 - JD10)/29.53085106382979 = 1.015711120717605
lunation fraction of Z11 = L - floor(L) = 0.0157111220717605 ≈ 0.3/19,
which also agrees with the above calculation.
It should be noted that the lunation fraction of the winter solstice is not an integer multiple of 1/19 as opposed to the case of many ancient six calendars. This is because there is no specified relationship between Z11 and the lunar conjunction at the epoch. Even in the Zhuanxu calendar, the conjunction and J1 were assumed to occur at midnight. Simple calculation shows that the lunation fraction of Z11 near the epoch was 69/152 = 8.625/19, which was also not an integer multiple of 1/19. As there is no specified relationship between any solar term and lunar conjunction at epoch C, there is no reason for the lunation fraction of Z11 to be an integer multiple of 1/19. The lunation fraction of any solar term increases by 7/19 (mod 1) every year. If it is not an integer multiple of 1/19 to begin with, it will never be in the subsequent years.
Next, we turn our attention to Z10. We can calculate it using equation (2), but Z10 in N-130 should be in the year -131. So y=-131 should be used in the calculation. In fact, we don't need to use equation (2) at all. Z10 was two solar terms before Z11, so we can simply subtract (2/24)Ps from Z11:
JDZ10 = JDZ10 - (2/24)×365.25 = 1673537.5 + 21/32.
Comparing JDZ10 and JD10, we see that it fell on the day before the New Year day of N-130. That was Nov. 24, 132 BCE. Z10 in 131 BCE must be on Nov. 24, 131 BCE, give or take one day. From Table 5, we see that the New Year day of N-129 was 30 days after Oct. 15, which was on Nov. 14, 131 BCE. This means that there was no Z10 in N-130.
Finally, let's compute J1, which was 3 solar terms after Z11. So
JDJ1 = JDZ11 + (3/24)×365.25 = 1673613.5 + 3/4,
L = (JDJ1 - JD10)/(29 + 499/940) = 2 + 5198/9253,
lunation fraction of J1 = 5198/9253 ≈ 10.7/19.
The xiǎoyú of J1 was 3/4. The Julian day at noon on the day of J1 was 1673614. The corresponding date in the proleptic Julian calendar was Feb. 8, 131 BCE and the sexagenary date was dīng hài. From Table 5 we can deduce that it fell on the 17th day in month 12 in the Han calendar.
Example 2: Calculate all months in N-201, the dates and lunation fractions of the solar terms Z10, Z11 (winter solstice) and Z5 (summer solstice).
From Table 4 we know that epoch A applies to the calendar before month 1 in N-201 and epoch B applies to the calendar beginning in month 1 in N-201. So we need to calculate A(-201) for both epoch A and epoch B.
Let's do the calculation for epoch A first. From Table 4, we find JD(M0) = 1589523.5, yz = -225 and ΔA = 1670. Hence we have
c = floor((-201 + 225)/19) = 1
k = -201 + 225 - 19 = 5
J(5) = 1, but epoch A is not valid after month 1. It is epoch B that determines if N-201 has a post month 9.
A(-201) = 1670 + 235 + 61 = 1966
JD10 = 1589523.5 + 1966×(29+499/940) = 1647580.5 + 614/940.
The xiǎoyú of the New Year day conjunction was 614 (omitting the denominator 940). The Julian day at noon on the New Year day was 1647581. The corresponding date in the proleptic Julian calendar was Oct. 31, 203 BCE and the sexagenary date was jiǎ wǔ.
As for epoch B, we have JD(M0)=1633701.5, yz=-225 and ΔA=174 from Table 4. Hence,
c = floor((-201 + 225)/19) = 1
k = -201 + 225 - 19 = 5
J(5) = 1 ⇒ there was a post month 9 in N-201.
A(-201) = 174 + 235 + 61 = 470.
Epoch B applies in month 1 in N-201, which was 3 months after month 10. So
JD1 = 1633701.5 + (470+3)×(29+499/940) = 1647669.5 + 87/940.
The xiǎoyú of the month 1 conjunction was 87. The Julian day at noon on the day of month 1 conjunction was 1647670. The corresponding date in the proleptic Julian calendar was Jan. 28, 202 BCE and the sexagenary date was guǐ hài. Now that we have the information on the month 10 conjunction and month 1 conjunction, the conjunction times associated with all other months in N-201 can be calculated by adding integer multiples of the lunar cycle. The following table summarizes the result.
| Chinese month | Conjunction date | xiǎoyú |
| 10 (L) | Oct. 31, 203 BCE (Jiǎ Wǔ) | 614 |
| 11 (S) | Nov. 30 (Jiǎ Zǐ) | 173 |
| 12 (L) | Dec. 29 (Guǐ Sì) | 672 |
| 1 (S) | Jan. 28, 202 BCE (Guǐ Hài) | 87 |
| 2 (L) | Feb. 26 (Rén Shēn) | 586 |
| 3 (S) | Mar. 28 (Rén Xū) | 145 |
| 4 (L) | Apr. 26 (Xīn Mǎo) | 644 |
| 5 (S) | May 26 (Xīn Yǒu) | 203 |
| 6 (L) | June 24 (Gēng Yín) | 702 |
| 7 (S) | July 24 (Gēng Shēn) | 261 |
| 8 (L) | Aug. 22 (Jǐ Chǒu) | 760 |
| 9 (S) | Sep. 21 (Jǐ Wèi) | 319 |
| post 9 (L) | Oct. 20 (Wù Zǐ) | 818 |
As mentioned above, the number of days in a month may be determined by the xiǎoyú of the conjunction. If the xiǎoyú is smaller than 441, the month has 29 days; otherwise, the month has 30 days. However, this rule did not necessarily apply to month 12 because the conjunction of month 12 was calculated from epoch A and the conjunction of month 1 was calculated from epoch B. So the number of days in month 12 must be determined by the number of days between the two conjunctions.
The computation of solar terms is the same as above. Let's begin with the winter solstice (Z11). It follows from equation (1) that the Julian day of Z11 in N-201 is given by
JDZ11 = 1721050.5 + 19/32 - 201×365.25 = 1647635.5 + 11/32.
The xiǎoyú was 11/32. The Julian day at noon on the day of Z11 was 1647636. The corresponding date in the proleptic Julian calendar was Dec. 25, 203 BCE and the sexagenary day was jǐ chǒu. From Table 6, we can determine that Z11 fell on the 26th day in month 11 in the Han calendar. Since Z11 was earlier than month 1, we must use the conjunctions in epoch A to calculate the lunation fraction. We use J10 to do the calculation below:
L = (JDZ11 - J10)/(29 + 499/940) = 1 + 189201/222072,
lunation fraction of Z11 = 189201/222072 ≈ 16.2/19.
Z10 was two solar terms before Z11, so
JDZ10 = JDZ11 - (2/24)×365.25 = 1647604.5 + 29/32.
The xiǎoyú was 29/32. The Julian day at noon on the day of Z10 was 1647605. The corresponding date in the proleptic Julian calendar was Nov. 24, 203 BCE and the sexagenary day was wù wǔ. From Table 6, we can determine that Z10 fell on the 25th day in month 10 in the Han calendar. Since Z10 was in month 10, its lunation fraction can be directly computed using J10.
Lunation fraction of Z10 = (JDZ10 - J10)/(29 + 499/940) = 182383/222072 ≈ 15.6/19.
The summer solstice (Z5) was half of solar cycle after the winter solstice. Hence,
JDZ5 = JDZ11 + 365.25/2 = 1647817.5 + 31/32.
The xiǎoyú was 31/32. The Julian day at noon on the day of Z5 was 1647818. The corresponding date in the proleptic Julian calendar was June 25, 202 BCE and the sexagenary day was xīn mǎo. From Table 6, we can see that the summer solstice fell on the second day in month 6 in the Han calendar. Since Z5 was after month 1, we need to use epoch B's conjunctions to calculate its lunation fraction. We use JD1 to do the calculation below.
L = (JDZ5 - JD1)/(29 + 499/940) = 5 + 9189/222072,
lunation fraction of Z5 = 9189/222072 ≈ 0.8/19.
It is well known that the conjunction times determined by calendars in the Qin and Early Han dynasties were later than the astronomical conjunction times. The average of the time differences was about one day. This explains why the recorded solar eclipses in the early Han dynasty often occurred one day (and sometimes two days) before the calendrical conjunction days. The lunar cycle in the sìfēn system is slightly longer than the synodic month. The conjunction times would be one day later, on average, after about 300 years. This is why it's obvious from the figure below that the time lags of the calendrical conjunctions appear to increase steadily.
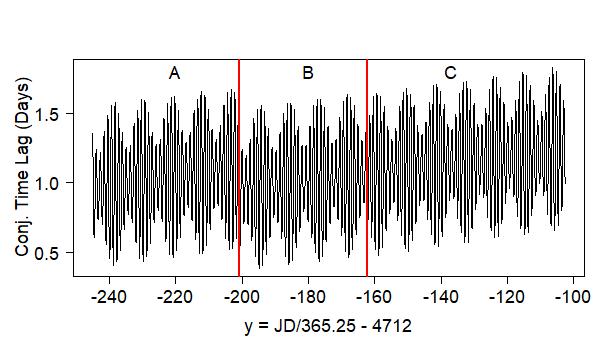
JDcalendrical - JDastronomical in units of days.fn5
The oscillation seen in the figure is caused by the píngshuò rule, which only takes into account the mean motions of the Sun and Moon. On average, the calendrical conjunctions were 1.03 days later than the astronomical conjunctions from N-245 to N-206. When the epoch was changed from A to B, the xiǎoyús of the conjunctions were shortened by 144/940, making the calendrical conjunctions about 0.15 days earlier. This was not enough to reduce the time lags of the calendrical conjunctions, but only temporarily delayed the increase of the time lags. When epoch B was changed to epoch C, the conjunction xiǎoyús were shortened by only 18/940, which was too small to have a noticeable effect. As a result, the time lags are seen to increase steadily. The average time lag of the calendrical conjunctions was 1.20 days between 134 BCE and 129 BCE, and increased to 1.24 days after 110 BCE. The average values given here are very close to the values given in Zhāng's paper in 2007Zhang07. The time lag was largely removed in the calendar reform in 104 BCE. Such serious time lags were impossible to miss and so the calendars were designed to behave this way.
In the book On the Calendric System of the Qin and Early Han DynastiesLi16, Lǐ Zhōnglín thinks that the calendar makers were strongly influenced by the "mandate of heaven" political doctrine. The epochs were chosen carefully to coincide with significant political events at the expense of reducing the discrepancies between the calendrical and astronomical conjunctions. For example, epoch A was in the year N-360, which coincided with the year when Duke Xiao of Qin (秦孝公) became the ruler of the Qin state. During his reign, Duke Xiao employed the legalist statesman Shang Yang (商鞅) to carry out a series of ground breaking political, military and economic reforms, transforming Qin into a dominant superpower in the Warring States period. Epoch C was in N-205, which coincided with the year when Liu Bang (劉邦), founder of the Han dynasty, attacked the Qin capital, leading to the surrendering of the Qin ruler and the collapse of the Qin dynasty.
It is easy to calculate the dates of solar terms in the reconstructed calendar and their lunation fractions using the method described above. The table on this page lists the data for the solar terms Z10, Z11, Z12, J1 and Z1 from N-245 to N-103. As demonstrated in Example 1 in the Section 4, some years might not have Z10. The Z10 column refers to the Z10 that was closest to the New Year day. We can see that some of the Z10's occurred in post month 9 of the previous year.
The lunation fraction of a solar term increased by 7/19 (mod 1) every year and it repeated with a cycle of 19 years. This was not the case for the dates of solar terms in the Chinese calendar. Take the winter solstice (Z11) as an example. In example 1 in Section 4, we find that the lunation fraction of Z11 in N-130 was 1163/74024 (≈ 0.3/19). This means that Z11 occurred 1163/74024 lunar cycles after the (month 11) conjunction. Using today's 24 hour system, Z11 occurred 11 hours 8 minutes and 6 seconds after the conjunction. We find that the xiǎoyú of the month 11 conjunction was 592 (denominator was 940), which means 15:06:54 using the 24-hour system. Adding 11 hours 8 minutes and 6 seconds to the conjunction time yields 02:15 on the next day. So Z11 occurred on the second day of month 11 in N-130. 19 years after N-130 was N-111. The lunation fraction of Z11 went through one cycle and returned to 1163/74024 again. So Z11 occurred 11 hours 8 minutes and 6 seconds after the month 11 conjunction again. There were 235 months in 19 years. So the xiǎoyú of the month 11 conjunction in N-111 was mod(592 + 235×499, 940) = 357 and the conjunction occurred at 09:06:54. Adding 11 hours 8 minutes and 6 seconds to the conjunction time yields 20:15. This means Z11 occurred on the same day as the month 11 conjunction in N-111, which was not on the same day in the Chinese calendar as in N-130. This result is consistent with the dates of Z11 listed on this page. So the dates of a solar term in the Chinese calendar didn't repeat with a 19-year cycle. From the discussion of the sìfēn system, we know that the cycle was 76 years (the bù cycle). Since none of the epochs A, B, and C was used for more than 76 years, it is necessary to list the dates for all years from N-245 to N-103.
From the table on this page, we see that before N-162, the dates of the winter solstice (Z11) were all in month 11 and all leap years coincided with the years in which the lunation fractions of Z11 (and Z12) were greater than 12/19. After N-162, the leap month pattern was interrupted and the dates of Z11 were no longer fixed to month 11. Instead, the dates of Z12 were all in month 12 and the dates of Z1 were all in month 1. The leap years after N-162 coincided with the years in which the lunation fractions of Z1 were greater than 12/19.
Even though the table on this page only lists a few solar terms. I have computed all 24 solar terms. I find that before N-162, only the dates of Z11 were fixed to a month and the leap years only coincided with the years in which the lunation fractions of Z11 and Z12 were greater than 12/19. After N-162, only the dates of Z12 and Z1 were fixed to a month and the leap years only coincided with the years in which the lunation fractions of Z1 were greater than 12/19. This information may provide an important clue to the intercalation rules used by the calendar systems from N-245 to N-103.
Footnotes and References
[fn1] The purpose of this page is to explain the reconstruction method adopted by this website. This is not a research paper. I did not search the literature to find all the relevant papers on this subject. I apologize if I omitted some important references.
[fn2] I have not been able to figure out how the dates in his Table 10 are calculated. If I know the date and xiǎoyú of any one of the conjunctions, I will be able to figure out the times of the other conjunctions using his adopted lunar cycle (29 + 663/1249) days. However, Table 10 only lists the sexagenary dates of the conjunctions but no information about the xiǎoyús. This problem is not difficult to solve. Let's focus on the first conjunction in the table, which was on Nov. 13, 207 BCE in the proleptic Julian calendar. The xiǎoyú of the conjunction can take one of the 1249 possible values: 0, 1/1249, 2/1249, ..., 1248/1249. There are 1262 conjunction dates between N-205 and N-104 listed in the table (omitting the last row for N-103). I can try these 1249 possible xiǎoyús one by one and see which one can produce the dates matching all of the listed 1262 dates. I wrote a simple computer code to carry out the calculation and found a unique solution: the xiǎoyú of the first conjunction was 611/1249. The xiǎoyú increases by 663 (mod 1249) each month. Since mod(611 + 195×663, 1249) = 0, the 196th conjunction in the table occurred at midnight. This conjunction occurred on Oct. 21, 191 BCE and its sexagenary day cycle was bǐng xū. This was the beginning of a bù cycle. Like the sìfēn system, a bù cycle may be named after the sexagenary name of its first day. The problem is that the name bǐng xū is not one of the names listed in the paper. A bù cycle in this system is 29×1249+663=36884 days. Since 36884×3=9221×12, the branch name of the bù cycle repeats every 3 cycles. If xū is a branch name, the other two names can only be wǔ and yín, but the 3 possible branch names listed in the paper are zǐ, shēn and chén. Clearly bǐng xū is incompatible with the names given in the paper.
If I assume that there are mistakes in Table 10, I could find a possible solution. The assumption is that the xiǎoyú of the first conjunction is 613/1249. If that is the case, there will be two mismatches when compared with the dates in Table 10: one is the month 5 conjunction in N-136, and the other is the month 12 conjunction in N-112. Interestingly, these two mismatched dates actually match the dates listed in Li12's calendar table. Since mod(613+860×663, 1249) = 0, the 861st conjunction occurred at midnight. This conjunction turns out to be the month 5 conjunction in N-136, one of the mismatched conjunction days. The sexagenary name of this conjunction day was changed from guǐ mǎo to jiǎ chén. Jiǎ chén is one of the names of the bù cycles listed in the paper. Unlike the sìfēn system, however, a bù cycle is a cycle for the time of lunar conjunction returning to its starting value, not a cycle in which both the conjunction and a solar term returning to their original values. Using the bù cycle 36884 days, I calculated the dates backward to see if there was any possible date on which a conjunction and a solar term both occurring at midnight that would result in the times of solar terms close to those of the Zhuanxu calendar. I found a possible epoch. It's at the time when J5 and conjunction were assumed to both occur at midnight on June 12, 6297 BCE (Julian day = -578393.5). The solar terms computed using this epoch are about 10 minutes earlier than those in the Zhuanxu calendar around 150 BCE. Since the adopted solar cycle is slightly shorter than that in the sìfēn system, the times of solar terms calculated using this epoch are about 15 minutes later than those in the Zhuanxu calendar around 206 BCE and about 30 minutes earlier around 104 BCE. Are the data in Table 10 computed using this epoch? Are there really mistakes in Table 10?[fn3] Using Epoch B in Li12, one can easily find that the sexagenary date of the month 5 conjunction in N-199 was jǐ mǎo, but it is also easy to see that the listed jǐ sì is wrong and jǐ mǎo is correct from his calendar table. According to his calendar table, the sexagenary dates of the month 4 and month 6 conjunction days in N-199 were both jǐ yǒu, which means that there were 60 days between month 4 and month 6 conjunctions. This is possible only if both month 4 and month 5 had 30 days. Thus, the sexagenary date of month 5 conjunction was 30 days after jǐ yǒu, which was jǐ mǎo.
[fn4] The calendar data in 3500 Years of Calendars and Astronomical Phenomena are based on: the Zhuanxu calendar before N-215, the author's reconstructed Han calendar based on the N-133 dataZhang78 from N-215 to month 12 in N-103, and the Tàichū astronomical system beginning in month 1 in N-103. The book does not provide this information. I deduce it by comparing the data in the book and data in the author's another book Tables of Chinese Calendars in the Pre-Qin PeriodZhang87. In 3500 Years of Calendars and Astronomical Phenomena, two consecutive short months appear in month 12 and month 1 in N-103. This is impossible under the píngshuò rule (based on the mean motions of the Moon and Sun), but is easily explained by the change of calendar in month 1.
[fn5] Astronomical conjunctions are calculated by the modern method. That is the method described in this pdf document, but precession has to be calculated using the Vondrák et. al. precession model described in Section 7.2 of the document. The computed TDB times are then converted to UT1 using the method described in Section 8 of the document. Julian days JD(Mi) of the calendrical conjunctions are calculated using equation (3) above. The resulting times are regarded as the local time. The capitals of Qin and Early Han dynasties were both close to the present-day city Xi'an. The longitude of Xi'an is 108.9°E. Hence the local time of the capitals was (108.9/15) hours = 0.3025 days ahead of UT1. Subtracting 0.3025 from JD(Mi) results in Julian day in UT1. Subtracting the UT1 Julian day of an astronomical conjunction from the UT1 Julian day of the corresponding calendrical conjunction gives the time lag. There were 1764 lunar conjunctions between the month 10 conjunction in N-245 and month 4 conjunction in N-103. Figure 1 was produced using these 1764 data points.
[Li09] Lǐ, Zhōnglín (李忠林), "On the Intercalary Method of the Calendar System of Qin and Early Han Dynasties" (试论秦汉初历法的置闰规则), Journal of Sichuan University (Social Science Edition) (四川大学学报(哲学社会科学版)), No. 6, 2009 (Sum No. 165), pp. 5–11.
[Li12] Lǐ, Zhōnglín (李忠林), "Qín zhì Hàn chū (qián 246 zhì qián 104) lì fǎ yán jiū — yǐ chū tǔ lì jiǎn wéi zhōng xīn" (秦至汉初(前246至前104)历法研究—以出土历简为中心 or "Researches on Calendars from Qin to early Han (246 B.C. to 104 B.C.) — centering on excavated calendrical bamboo slips"), in Zhōng guó shǐ yán jiū (《中国史研究》 or Studies in Chinese History), issue no. 2, pp. 17–69 (2012).
[Li16] Lǐ, Zhōnglín (李忠林), On the Calendric System of the Qin and Early Han Dynasties (Chinese), Zhonghua Book Company (Beijing), January 2016.
[Zhang78] Zhāng, Péiyú (張培瑜), "Hàn chū lì fǎ tǎo lùn" (汉初历法讨论 or "On the calendar system in the early Han dynasty"), in Zhōng Guó Tiān Wén Xué Shǐ Wén Jí (《中国天文学史文集》 or A Collection of Essays on the History of Chinese Astronomy), Science Press (Beijing), April 1978, pp. 82–94.
[Zhang87] Zhāng, Péiyú (張培瑜), Zhōng Guó Xiān Qín Shǐ Lìbiǎo (《中国先秦史历表》 or Tables of Chinese Calendars in the Pre-Qin Period), Shandong Qilu Press, June 1987.
[Zhang97] Zhāng, Péiyú (張培瑜), Sānqiān Wǔbǎiniǎn Lìrì Tiānxiàng (《三千五百年历日天象》 or 3500 Years of Calendars and Astronomical Phenomena), Elephant Press, July 1997.
[Zhang07] Zhāng, Péiyú (張培瑜), "Gēn jù xīn chū lì rì jiǎn dú shì lùn Qín yǔ Hàn chū de lì fǎ" (根据新出历日简牍试论秦与汉初的历法 or "An Attempt to Discuss the Calendrics of the Qin and Early Han According to Newly Excavated Calendars on Slips and Boards"), in Zhōngyuán wénwù (《中原文物》 or Culture relic in Central Plains China), issue no. 5, pp. 62–77 (2007).
[ZCBH08] Zhāng, Péiyú (張培瑜), Chén, Měidōng (陳美東), Bó, Shùrén (薄樹人), and Hú, Tiězhū (胡鐵珠), Zhōng Guó Gǔdài Lìfǎ (《中国古代历法》 or Ancient Chinese Calendars and Almanacs), China Science Press (Beijing), March 2008.