秦 与 汉 初 (公 元 前 221 年 – 前 104 年) 历 法 的 复 原 方 法
初稿: 2019年4月
本文细述本网站对秦至汉初(公元前221年–前104年)历法的计算,历法的复原方法采用李忠林在2012年发表的「秦至汉初(前246至前104)历法研究—以出土历简为中心」李忠林12(也可参看李忠林2016年的著作《秦至汉初历法研究》李忠林16)。复原方法的有效年限估计是从前246年至前104年,但是本网站只用在前221年至前104年。此复原法的要旨是把秦至汉初分为三个时段,每个时段有各自的合朔历元,然后用四分术的朔策计算每个时段的合朔时刻,置闰按照3-3-3-2-3-3-2的年序经验法则在十九年置七个闰月,但在汉文帝后元元年(公元前163年)起改变了章周的起算年李忠林09。二十四节气的时刻则与古六历之一的颛顼历相同。按李忠林的说法,置闰采用经验法则,二十四节气与闰月规则毫不相干,这点我认为值得再探讨,但这和复原历法没有直接关系,不在这里讨论。
本文所述的复原方法涉及古六历和本网站之古六历计算法,这些资料在本网站的古六历网页有叙述,这里就不重复了。
历代学者对于秦至汉初的历法一直感到困惑。《史记》说汉初沿用秦朝历法,《汉书》进一步说明所用的历法是古六历之一的颛顼历。但是历代学者已发现用颛顼历推算出的汉初历日与文献常有不合,而多与殷历相合。自宋人刘羲叟到近代学者陈垣,都主张秦与汉初的历法是颛顼历或殷历。到了1972年,在山东省临沂市银雀山汉墓出土了《元光元年历谱》,我们因此得知汉武帝元光元年(公元前134年)的历日,历谱所载的十三个朔日干支有十个与殷历合,有七个与颛顼历合,说明元光元年历谱所用的历法既不是颛顼历,也不是殷历,于是掀起了秦与汉初历法研究的热潮,学者们寻求一套历法复原方法以符合《元光元年历谱》。
汉初历法虽然不是古六历的任何一种历法,但一般认为应该仍是采用古六历的四分术。秦与汉初的历法用颛顼历的月序,以十月为一年之始,月序数是十月、十一月、十二月、正月、二月……九月,闰月置于年终,称为「后九月」,这点也是没有争议的。问题是只根据《元光元年历谱》不能找出以四分术为本的唯一复原方法。据张培瑜在《中国古代历法》张陈薄胡第三章第九节和「根据新出历日简牍试论秦与汉初的历法」张培瑜07所述,以《元光元年历谱》复原汉初历法有58种可能,合朔时刻的上下限可相差87分钟,在没有其他资料的情况下无法判断谁对谁错,很多学者都提出各自的复原方法。上世纪八十年代及以后,情况又有了新进展。先是在湖北江陵县张家山247号汉墓发现了从汉高祖五年(公元前202年)到高后二年(前186年)十七年的历日竹简,后来又在湖北省沙市区关沮乡清河村周家台30号秦墓出土的秦简、和在湖南西部里耶镇出土的秦简都有秦朝的历日资料。从这些考古新发现我们得知秦与汉初施行的历法比以前认识的复杂,先前没有一家的复原法能与新出土的历日完全吻合。
据我所知,目前有两篇文章尝试用这些新出土的简牍复原秦与汉初的历法注一。其一是上面提及的张培瑜在2007年发表的「根据新出历日简牍试论秦与汉初的历法」张培瑜07,另一是李忠林在2012年发表的「秦至汉初(前246至前104)历法研究—以出土历简为中心」李忠林12。李忠林的研究成果也发表在其著作《秦至汉初历法研究》李忠林16,笔者感谢李忠林教授赠送此书。两者都认为秦与汉初的历法不同,而张家山竹简历日所依据的汉初历法与《元光元年历谱》用的汉武帝时期历法又不相同,但两篇文章提出的历法复原方法不同。
张培瑜对秦朝历法的复原法采用四分术的朔策和岁实,以公元前606年(乙卯)己巳夜半霜降合朔齐同为历元(公历日期是前607年10月27日),并以小雪固定在十月为置闰标准。复原历法与已公布的考古发现及文献记载的(由秦昭襄王末年到秦亡)秦国历日都相符。文章的表九载有从秦王政元年(公元前246年)到秦亡(前207)的朔闰表。
至于汉初的历法,张培瑜的结论是不可能找到一种以四分术为本的历法可以完全满足从汉初到太初改历前这102年的全部历日。也就是说,如果汉初施行的历法确是四分术,则其间历法必有修改过;如果汉初的历法没有修改过,则这历法一定不是四分术。张培瑜试图打破四分术的框架,以一种平朔法来复原汉初历法。他假设的朔策是(29+663/1249)日,岁实是365.2496734日或(365+311.8420766/1249)日。这样的岁实看似莫明其妙,其实只是朔策的235/19倍,写成(365+5925/23731)日也可以。用235:19的比例显然是为了符合十九年七闰的章周规律。张培瑜没有明确说明复原历法的历元,但文章的表十给出从汉高祖元年(公元前206年)到汉武帝元封六年(前105年)的朔闰表注二。文章也没有说明复原历法的置闰法则,但有提及另一复原历法的置闰法则是把立春固定在正月,这是相当奇怪的置闰法则,而且明显不符合文末表十的朔闰表。我根据张培瑜在《中国古代历法》张陈薄胡第三章第九节所述的置闰法则得出正确的闰月。这法则是在汉文帝后元元年(公元前163年)前把冬至固定在十一月,在后元元年后则把雨水固定在正月。
张培瑜用非四分术的方法复原汉初历法,颇似他对春秋时期鲁国历法的复原(张培瑜的春秋历复原法可参考《中国古代历法》张陈薄胡第三章第五节,本网站的春秋历就是采用这复原方法,详情可参阅春秋历网页。)。张培瑜并没有给出汉初行用非四分术的论据,我应为这做法只是数据拟合的模型,不是汉初行用历法的依据。
李忠林在「秦至汉初(前246至前104)历法研究—以出土历简为中心」李忠林12提出另一复原方法。他认为既然秦、汉初与汉武帝时期的历日资料显示这三段时间行用的历法不同,最简单的解释是历法在这段期间至少有过兩次改动。他于是用三种以四分术为本的历法复原秦至汉初一百四十多年间的历法,三种历法以A、B、C名之。他主张三历法都用颛顼历的方法计算二十四节气,只是合朔计算采用三个历元。历法A的历元是秦孝公元年(公元前361年)十月丁巳朔无余(公历日期是前362年11月18日),历法B的历元是公元前240年十月乙亥朔无余(公历日期是前241年10月31日),历法C的历元是公元前206年十一月丁巳朔无余(公历日期是前207年12月14日)。「朔无余」是指合朔小余是零,即合朔发生在夜半(午夜零时)。历法A的行用时间暂定为秦王政以前到汉高祖五年十二月,历法B从汉高祖五年正月到文帝前元十六年后九月,历法C从文帝后元元年十月到太初元年五月。
李忠林对于秦与汉初的置闰法则有独特见解,认为置闰只是按照3-3-3-2-3-3-2的年序经验法则在十九年置七个闰月,但在汉文帝后元元年(公元前163年)起改变了章周的起算年。其实,李忠林在2009年的文章「试论秦汉初历法的置闰规则」李忠林09已指出秦至汉初的所有闰月皆可从出土历简与存世文献推出来,所以虽然我们不知道当时行用的置闰法则,但是仍能根据推出来的闰月复原历法。
张培瑜与李忠林两人提出的秦与汉初历法复原方法虽然不同,但是比较他们提供的朔闰表发现在140多年间、1700多个朔日里,只有19个朔日有差异,现在把这19个差异列于下表以供参考。表中的年份除了给出中国传统的帝王或年号纪年外,还用Ny表示年首最接近公元y年1月1日的历年。例如N-202表示汉高祖四年,始于公元-203年(即前204年)11月11日、终于-202年10月30日。
| 年份 | 月份 | 朔日 — 张培瑜 | 朔日 — 李忠林* |
|---|---|---|---|
| N-245 秦王政元年 | 二 | 戊申 (-245年3月5日) | 丁未 (-245年3月4日) |
| N-239 秦王政七年 | 九 | 庚子 (-239年9月21日) | 己亥 (-239年9月20日) |
| N-232 秦王政十四年 | 三 | 壬辰 (-232年4月9日) | 辛卯 (-232年4月8日) |
| N-226 秦王政二十年 | 后九 | 甲申 (-226年10月27日) | 癸未 (-226年10月26日) |
| N-204 汉高祖二年 | 十 | 辛巳 (-205年11月3日) | 壬午 (-205年11月4日) |
| N-204 汉高祖二年 | 十二 | 庚辰 (-204年1月1日) | 辛巳 (-204年1月2日) |
| N-204 汉高祖二年 | 二 | 己卯 (-204年2月29日) | 庚辰 (-204年3月1日) |
| N-203 汉高祖三年 | 二 | 癸卯 (-203年3月19日) | 甲辰 (-203年3月20日) |
| N-203 汉高祖三年 | 四 | 壬寅 (-203年5月17日) | 癸卯 (-203年5月18日) |
| N-202 汉高祖四年 | 七 | 乙丑 (-202年8月3日) | 丙寅 (-202年8月4日) |
| N-202 汉高祖四年 | 九 | 甲子 (-202年10月1日) | 乙丑 (-202年10月2日) |
| N-183 汉高后四年 | 二 | 丁丑 (-183年3月8日) | 戊寅 (-183年3月9日) |
| N-177 汉文帝前元二年 | 九 | 己巳 (-177年9月25日) | 庚午 (-177年9月26日) |
| N-170 汉文帝前元九年 | 三 | 辛酉 (-170年4月13日) | 壬戌 (-170年4月14日) |
| N-163 汉文帝前元十六年 | 十 | 癸丑 (-164年10月30日) | 甲寅 (-164年10月31日) |
| N-136 汉武帝建元四年 | 五 | 癸卯 (-136年5月26日) | 甲辰 (-136年5月27日) |
| N-129 汉武帝元光五年 | 十一 | 乙未 (-130年12月13日) | 丙申 (-130年12月14日) |
| N-112 汉武帝元鼎四年 | 十二 | 丙戌 (-112年1月4日) | 丁亥 (-112年1月5日) |
| N-106 汉武帝元封四年 | 七 | 戊寅 (-106年7月23日) | 己卯 (-106年7月24日) |
* 李忠林朔闰表中汉高祖七年五月朔的日干支有误:己巳应改为己卯注三,这错误在《秦至汉初历法研究》李忠林16改正了。
鉴于两套复原方法都能完全符合已出土的历简和传世文献,而且差异不大,二者可任选其一。仔细比较两套算法,我认为李忠林的方法较为可取,所以本网站采用他的复原方法。下面各节详细说明本网站的具体计算方法。
复原历法的二十四节气和颛顼历相同,计算方法在古六历网页已有叙述,这里只把公式列出。根据古六历网页公式(4)和表二的数据,可得最接近公历y年1月1日的冬至儒略日数是
JD(W(y)) = 1721050.5 + 19/32 + y·Ps (1)
其中Ps=365.25是四分术的岁实。其他二十四节气的儒略日数可用古六历网页公式(5)计算:
JDq(j, y) = JD(W(y)) + (j/24)·Ps (2)
其中j是从冬至算起的节气数,以j=0表示冬至、j=1表示小寒、j=2表示大寒、j=3表示立春……j=23表示大雪(二十四节气的名称和次序可参阅本网站的二十四节气网页)。式中除了冬至落在y-1年的12月末外,其余节气都在公元y年。
合朔的儒略日数也可以写成古六历网页中的公式(1):
JD(Mi) = JD(M0) + i·PL (3)
式中PL=(29+499/940)是四分术的朔策,i是从历元合朔M0起算的积月,Mi是从历元合朔M0起算的第i个合朔,JD(M0) 是历元合朔M0的儒略日数。
上节说过复原历法采用三个合朔历元。以历法A为例,历元取秦孝公元年(公元前361年)十月丁巳朔无余。用上一节定义的历年记号,秦孝公元年是N-360,颛顼历的十月朔是公元前362年11月17日,日干支是丙辰,比历法A的历元早一日。公元前362年11月18日(丁巳日)夜半的儒略日数是1589523.5,由此得出历法A的JD(M0)=1589523.5。历法B和C的JD(M0)也可用类似的方法计算,结果列于下表。
| 历 法 A | 历 法 B | 历 法 C | |
|---|---|---|---|
| 历元 | N-360十月丁巳朔无余 | N-239十月乙亥朔无余 | N-205十一月丁巳朔无余 |
| 行用时间 | N-245(秦王政元年)之前 – N-201(汉高祖五年)十二月 | N-201(汉高祖五年)正月 – N-163(文帝前元十六年)后九月 | N-162(文帝后元元年)十月 – N-103(武帝太初元年)五月 |
| JD(M0) | 1589523.5 | 1633701.5 | 1646163.5 |
如果知道了从历元合朔到历年Ny十月朔的积月 A(y),Ny的十月朔便可用公式(3)把i换成A(y)求得,Ny的其他月份也可轻易计算。但是要知道A(y)的数值就要知道Ny之前的闰月分布。下一节探讨计算闰月和A(y)的方法。
在第一节(引言)已提及秦至汉初一百四十多年间的所有闰月都可从出土历简和存世文献推出来,所以即使不知道当时行用的置闰法则也能根据闰月的实际分布复原秦至汉初的历法,本网站就是以这原则处理秦至汉初的闰月。
年首积月A(y)可用类似本网站复原春秋历网页所述的方法计算。由于春秋时期鲁国的历法没有固定的置闰规则,闰月和A(y)都必须根据闰月的实际年份逐年计算。秦至汉初历法的闰月则分布规整,而且符合古六历网页所述的3-3-3-2-3-3-2年份次序,只是在汉文帝后元元年(N-162)起改变了章周的起算年(详情可参阅李忠林的「试论秦汉初历法的置闰规则」李忠林09),所以闰月和A(y)不须要如春秋历般逐年计算,只要掌握了一章周内十九年的数据便可推出其他年份的闰月和A(y)。具体的计算方法是先定义两个函数J和R:
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| J(k) | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| R(k) | 0 | 12 | 24 | 37 | 49 | 61 | 74 | 86 | 98 | 111 | 123 | 136 | 148 | 160 | 173 | 185 | 197 | 210 | 222 |
此处k是从某一章首起算的积年:k=0表示章周的第一年、k=1表示章周的第二年、k=2表示章周的第三年、……、k=18表示章周的第十九年。J(k)的数值表示该年有没有闰月(即后九月):J(k)=0表示没有闰月、J(k)=1表示有闰月。表中的0、0、1、0、0、1、0、0、1、0、1、0、0、1、0、0、1、0、1正是3-3-3-2-3-3-2的闰月规律。R(k)是从章周第一年第一个月起算的年首积月,R(k)可用以下递归公式计算:
R(0) = 0, R(k) = R(k-1) + 12 + J(k-1) (k=1, 2, ..., 18) (4)
也就是说年首积月第一年是0,其后每年增加12或13:没有闰月就增加12、有闰月则增加13。表三所列的R(k)就是用递归公式(4)计算的结果。有了J(k)和R(k)两个函数后,年首到历元的积月A(y)可用以下公式计算:
c = floor( (y - yz)/19 ) (5)
k = y - yz - 19c (6)
闰月: 如果J(k)=0就没有闰月、如果J(k)=1就有闰月 (7)
年首积月: A(y) = ΔA + 235c + R(k) (8)
其中floor(x)表示不小于x的最大整数,yz是 某一章首的年份。如前述,汉文帝后元元年改变了章周的起算年,所以yz在文帝后元元年前和后元元年后的数值不同。c就是从yz算起到y对上一个章首的周期数。式(6)中k是从y到对上一个章首的积年,写成k = mod(y - yz, 19)也可以,此处mod(X,Y)指X除以Y后所得之余数。公式(8)的最后两项代表从yz到y的积月,但是A(y)是从历元到y的积月,所以要加上修正值ΔA。ΔA和yz在历法A、B、C的数值列于下表,为方便查阅,这里把表二的资料也一并列出。如上述,yz在汉文帝后元元年前后取不同数值,但汉文帝后元元年正是历法C的起用年,故yz在历法A和B取同一数值,在历法C取另一数值。
| 历 法 A | 历 法 B | 历 法 C | |
|---|---|---|---|
| 历元 | N-360十月丁巳朔无余 | N-239十月乙亥朔无余 | N-205十一月丁巳朔无余 |
| 行用时间 | N-245(秦王政元年)之前 – N-201(汉高祖五年)十二月 | N-201(汉高祖五年)正月 – N-163(文帝前元十六年)后九月 | N-162(文帝后元元年)十月 – N-103(武帝太初元年)五月 |
| JD(M0) | 1589523.5 | 1633701.5 | 1646163.5 |
| yz | -225 | -225 | -179 |
| ΔA | 1670 | 174 | 321 |
有了公式(1)–(3)、(5)–(8)、表二、表三和表四的数据就可以计算秦至汉初一百四十多年间的历法,下一节用两个例子展示实际的计算。
虽然复原历法有效年限估计是秦王政元年前到汉武帝太初元年五月,本网站年历网页从公元-220年(即前221年)起才用复原历法、朔闰表网页则从N-220年(即秦始皇二十六年)起才用复原历法(年历网页以公历为主、朔闰表网页则以农历为主)。两网页都在汉武帝太初元年五月起改用张培瑜《三千五百年历日天象》张培瑜97的数据注四。复原历法的太初元年三月是小月、四月是大月、五月是小月。改了历法后,五月朔提前了一天,使四月变成小月,而新历法的五月又是小月,于是出现了三、四、五三个相连小月,这在平朔法则是不可能的,只有在改历时才可能出现。如果在太初元年六月才改用太初历,就会使五月只有二十八日,这在平时也是不可能出现的。
例一:计算N-130(汉武帝元光四年)的所有月份,以及小雪、冬至、立春的日期和月龄。
先计算月份。根据表四,N-130应用历法C、JD(M0)取1646163.5、yz = -179、ΔA = 321。用公式(5)–(8)及表三得出:
c = floor( (-130 + 179)/19) = 2
k = -130 + 179 - 19×2 = 11
J(11) = 0 ⇒ N-130没有后九月
A(-130) = 321 + 235×2 + 136 = 927。
有了年首积月后,N-130十月朔的儒略日数用公式(3)把i=A(-130)计算:
JD十月朔 = 1646163.5 + 927×(29+499/940) = 1673538.5 + 93/940
合朔小余是93(略去分母940),用现行的时间系统即是说合朔时间是2时22分28秒。朔日正午的儒略日数是1673539,用儒略日转公历的标准方法(例如理查斯算法)算出对应的公历日期是公元前132年11月25日,用干支网页的公式求得朔日的天干数是
1 + mod(1673539-1, 10) = 9,日天干是壬;朔日的地支数是
1 + mod(1673539+1, 12) = 9,日地支是申,所以朔日干支是壬申。
N-130的其他月份的合朔日期和小余只须把十月朔的时刻加上朔策的整数倍便可求得。传统的计算法是用大小余,日数先定为29,把合朔小余加499(略去分母940),如果大于940则减去940并把日数进一得30,下一个朔日便是29日或30日后。例如十月朔是壬申,小余93,把小余加499得592,日数是29,所以十月是小月,十一月朔在壬申日后29日。29=3×10-1,所以天干是壬之前的第一个天干,即辛;29=2×12+5,所以日地支是申之后的第五个地支(数到亥后回到子再数),即丑。因此十一月朔是辛丑,小余是592。公历日期是11月25日之后29日,即11月(25+29)日=12月(25+29-30)日=12月24日。当然,传统算法在编写程式上会较为麻烦,不及儒略日数那么方便。下表把十月至九月的合朔日期、干支和小余列出。
| 月份 | 朔日公历日期 | 朔日干支 | 合朔小余 |
| 十(小) | 前132年11月25日 | 壬申 | 93 |
| 十一(大) | 前132年12月24日 | 辛丑 | 592 |
| 十二(小) | 前131年1月23日 | 辛未 | 151 |
| 正(大) | 2月21日 | 庚子 | 650 |
| 二(小) | 3月23日 | 庚午 | 209 |
| 三(大) | 4月21日 | 己亥 | 708 |
| 四(小) | 5月21日 | 己巳 | 267 |
| 五(大) | 6月19日 | 戊戌 | 766 |
| 六(小) | 7月19日 | 戊辰 | 325 |
| 七(大) | 8月17日 | 丁酉 | 824 |
| 八(小) | 9月16日 | 丁卯 | 383 |
| 九(大) | 10月15日 | 丙申 | 882 |
月大月小由两朔日之间的日期间隔决定,两朔日相差二十九日为小月、三十日为大月。合朔小余是合朔离子正的时间以分数日表示,分母940往往略去。由于朔策是(29+499/940)日,每月的合朔小余是前月的小余加上499,达到或超过940则减去940,合朔小余如果小于441,加了499后仍小于940,则此月是小月,大于或等于441时则是大月。
现在计算小雪、冬至、立春的日期和月龄,先计算冬至。用公式(1)求得N-130冬至的儒略日数是
JD冬至 = JD(W(-130)) = 1721050.5 + 19/32 -130×365.25 = 1673568.5 + 3/32
冬至小余是3/32,冬至日正午的儒略日数是1673569,用上述的方法计算出对应的公历日期是公元前132年12月25日、日干支是壬寅,从表五可见冬至在十一月初二。至于冬至的月龄,按定义是冬至离之前的合朔时间,这里用朔策的分数倍表示。冬至之前的朔是十一月朔。
JD十一月朔 = JD十月朔 + 29 + 499/940 = 1673567.5 + 592/940,
冬至月龄 = (JD冬至 - JD十一月朔)/(29 + 499/940) = 1163/74024 ≈ 0.3/19。
以上的计算保留了分数,只是为了方便展示小余的数值而已。其实本网站的历法计算全部用十进制小数,我在古六历网页的最后一节有详细叙述,其中最后一个公式给出二十四节气月龄的简易计算法:
L = (JD - JD(M0))/29.53085106382979 (9)
节气月龄 = L - floor(L) (10)
式中JD(M0)可从表二查得,历法C的值是1646163.5。L是从历元合朔M0起算到该节气的时间间隔以朔策为单位,月龄是节气与上一个合朔的时间间隔,以朔策为单位就是L的小数部分。以冬至为例,
L = (JD冬至 - 1646163.5)/29.53085106382979 = 928.0157111207177
冬至月龄 = L - floor(L) = 0.01571112207177 ≈ 0.3/19,与上面计算的数值一致。
其实每一个合朔的懦略日数都是JD(M0)加上朔策的整数倍,所以用任何一个合朔计算L都可以,得到的L只是整数部分不同而已。这里就再以JD十月朔为例:
L = (JD冬至 - JD十月朔)/29.53085106382979 = 1.015711120717605
冬至月龄 = L - floor(L) = 0.0157111220717605 ≈ 0.3/19,也与上面计算的一致。
值得注意的是在古六历很多历法里,冬至的月龄往往是1/19的整数倍,但在这里却不是,这是因为历元气朔并没有冬至闰余无的关系。即使在颛顼历,历元气朔的关系是夜半立春合朔齐同,由此可算出颛顼历冬至在历元年份的月龄是69/152=8.625/19,也不是1/19的整数倍,而历法C的历元干脆不指定气朔有任何关系,不是1/19的整数倍是正常的。月龄每年增加7/19(大于或等于一就把一减去),所以其他年份的月龄也不会是1/19的整数倍。
其他二十四节气可用公式(2)计算。N-130的小雪应在公元-131年,所以应用y=-131来算,但是其实不一定要用公式(2)计算:小雪是冬至之前的第二个节气,只须把JD冬至减去(2/24)Ps就可以了。
JD小雪 = JD冬至 - (2/24)×365.25 = 1673537.5 + 21/32
比较JD小雪和JD十月朔,得知小雪日在十月朔日之前一日,即11月24日,不属于N-130。从表五可见N-129年首在前131年10月15日之后30日,即11月14日,而公元前131年的小雪必然在11月24日或前后一日,也就是说N-130没有小雪。
立春是冬至之后的第三个节气,所以
JD立春 = JD冬至 + (3/24)×365.25 = 1673613.5 + 3/4
L = (JD立春 - JD十月朔)/(29 + 499/940) = 2 + 5198/9253
立春月龄 = 5198/9253 ≈ 10.7/19。
立春小余是3/4,立春日正午的儒略日数是1673614,对应的公历日期是前131年2月8日、日干支是丁亥,从表五可算出在汉历的十二月十七。
例二:计算N-201(汉高祖五年)的所有月份,以及小雪、冬至、夏至的日期和月龄。
从表二得知N-201正月前用历法A,正月开始用历法B,所以历法A和B的积月都要计算。
先算历法A,根据表四,JD(M0)=1589523.5、yz=-225、ΔA=1670。
c = floor((-201 + 225)/19) = 1
k = -201 + 225 - 19 = 5
J(5) = 1,但历法A只用到十二月,N-201有没有后九月由历法B决定。
A(-201) = 1670 + 235 + 61 = 1966
JD十月朔 = 1589523.5 + 1966×(29+499/940) = 1647580.5 + 614/940
十月朔小余是614,朔日正午的儒略日数是1647581,对应的公历日期是前203年10月31日、日干支是甲午。
至于历法B,根据表四,JD(M0)=1633701.5、yz=-225、ΔA=174。
c = floor((-201 + 225)/19) = 1
k = -201 + 225 - 19 = 5
J(5) = 1 ⇒ N-201有后九月
A(-201) = 174 + 235 + 61 = 470
历法B从正月开始使用,正月是十月后的第三个月,所以
JD正月朔 = 1633701.5 + (470+3)×(29+499/940) = 1647669.5 + 87/940。
正月朔小余是87,朔日正午的儒略日数是1647670,对应的公历日期是前202年1月28日、日干支是癸亥。有了十月和正月的日期和朔小余后,N-201其他月份的合朔只须加上朔策的整数倍即得,下表列出计算结果。
| 月份 | 朔日公历日期 | 朔日干支 | 合朔小余 |
| 十(大) | 前203年10月31日 | 甲午 | 614 |
| 十一(小) | 11月30日 | 甲子 | 173 |
| 十二(大) | 12月29日 | 癸巳 | 672 |
| 正(小) | 前202年1月28日 | 癸亥 | 87 |
| 二(大) | 2月26日 | 壬辰 | 586 |
| 三(小) | 3月28日 | 壬戌 | 145 |
| 四(大) | 4月26日 | 辛卯 | 644 |
| 五(小) | 5月26日 | 辛酉 | 203 |
| 六(大) | 6月24日 | 庚寅 | 702 |
| 七(小) | 7月24日 | 庚申 | 261 |
| 八(大) | 8月22日 | 己丑 | 760 |
| 九(小) | 9月21日 | 己未 | 319 |
| 后九(大) | 10月20日 | 戊子 | 818 |
如上述,月大月小可从小余数值得知,小余小于441是小月,否则是大月。但是这规则不一定适用于十二月,因为正月开始改用新历法,所以必须从十二月朔和正月朔日期间隔定出十二月是大月还是小月。
节气的计算与上面一样。先算冬至,用公式(1)求得N-201冬至的儒略日数是
JD冬至 = 1721050.5 + 19/32 - 201×365.25 = 1647635.5 + 11/32。
冬至小余是11/32,冬至日正午的儒略日数是1647636,对应的公历日期是前203年12月25日、日干支是己丑,从表六可算出冬至在汉历的十一月廿六。由于冬至在正月之前,计算月龄时应用历法A的合朔,这里且用JD十月朔来算:
L = (JD冬至 - JD十月朔)/(29 + 499/940) = 1 + 189201/222072
冬至月龄 = 189201/222072 ≈ 16.2/19。
小雪是冬至之前第二个节气,所以
JD小雪 = JD冬至 - (2/24)×365.25 = 1647604.5 + 29/32
小余是29/32,正午儒略日数是1647605,对应的公历日期是前203年11月24日,日干支是戊午,从表六可算出在汉历的十月廿五。由於小雪就在十月,用JD十月朔计算月龄最直接。
小雪月龄 = (JD小雪 - JD十月朔)/(29 + 499/940) = 182383/222072 ≈ 15.6/19。
夏至在冬至之后半个岁实,所以
JD夏至 = JD冬至 + 365.25/2 = 1647817.5 + 31/32
小余是31/32,正午儒略日数是1647818,对应的公历日期是前202年6月25日,日干支是辛卯,从表六可知在汉历的六月初二。夏至在正月之后,算月龄时要用历法B的合朔,这里就用JD正月朔来算。
L = (JD夏至 - JD正月朔)/(29 + 499/940) = 5 + 9189/222072
夏至月龄 = 9189/222072 ≈ 0.8/19。
秦与汉初的历法是后天的,即历法的合朔时刻迟于真正的合朔时刻,如下图所示,两者相差的平均值约为一天,所以汉初的日食多发生在晦日(即朔之前一天),甚至晦日前一天。四分术的朔策比朔望月的平均值稍大,积三百年就会后天一日,所以在图中明显可见后天日数有逐渐增大的趋势。
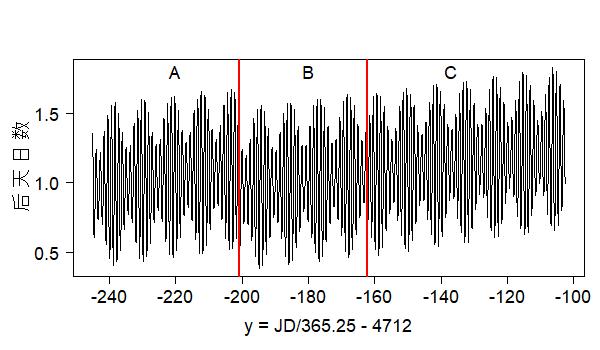
图中所见的波动是因为历法的合朔计算用平朔法,没有计及月亮和太阳的不均匀运动。从秦王政元年到秦朝灭亡之间,历法后天日数的平均值是1.03日。历法A改为历法B后,合朔小余调小了144/940(≈ 0.15日),不足以改变历法A的后天,只能暂缓后天日数之增长。历法B改为历法C后,合朔小余调小了18/940(≈ 0.019日),更是无补于事。所以历法后天的日数继续增加,汉武帝元光年间(前134年至前129年)的平均后天日数是1.20日,到了汉武帝元封元年(前110年)以后后天日数增加到1.24日,直到太初元年改历后才改正过来。这些平均后天日数的数值与张培瑜「根据新出历日简牍试论秦与汉初的历法」张培瑜07给出的数值很接近。历法后天如此严重,当时不可能不知道,而应该是故意的。
李忠林在《秦至汉初历法研究》李忠林16分析指出历法后天极可能受到天命论的政治思想影响,历法家选取历元,往往为了显示统治者合乎天命而舍弃较为合天的历元。例如历法A的历元选秦孝公元年就有强烈的天命论色彩,秦孝公在位期间采纳商鞅的变法使秦国富国强兵。历法C的历元是汉高祖元年,也有明显的天命论色彩。到了汉武帝太初元年的历改天命论色彩更加浓厚,这点在《秦至汉初历法研究》和《中国古代历法》张陈薄胡都有详细说明。
用上述方法可轻易算出二十四节气在秦至汉初一百四十多年间的日期和月龄,其中小雪、冬至、大寒、立春和雨水的数据列于此网页。正如上二节例一所示,某些年份有时没有小雪,表中所列的数据是最接近当年十月初一的小雪。从表中可见有一些小雪出现在前一年的后九月末。
节气的月龄每年增加7/19 (mod 1),十九年循环一周,但是节气的中历日期却不然。以冬至为例,上二节例一算得冬至在N-130(汉武帝元光四年)的月龄是1163/74024(≈0.3/19),也就是说冬至在合朔之后1163/74024个朔策,用现在通用的24小时制来说,冬至在合朔以后11小时8分6秒。例二亦算出十一月朔小余是592(分母是940),换成24小时制,合朔发生在15:06:54,把这时间加上11小时8分6秒,便得冬至时刻是朔日下一天的02:15,所以元光四年的冬至在十一月初二。十九年后是N-111(汉武帝元鼎五年),这时冬至的月龄已循环一周又回到1163/74024,即冬至仍在合朔后11小时8分6秒,这时的十一月朔是N-130十一月朔之后235个月,朔小余是mod(592 + 235×499, 940) = 357,合朔发生在09:06:54,把这时刻加上11小时8分6秒,得知冬至在朔日当天的20:15,所以是十一月初一,和元光四年的冬至日期不一样,这计算与此网页的数据吻合。可见节气的中历日期并非以十九年为周期,用四分术的法数可知周期是一蔀,即七十六年。由于历法A、B和C没有一部的行用时间超过七十六年,所以有必要把一百四十多年的数据全部列出。
从表中可看到在文帝后元元年(N-162)以前,冬至一直固定在十一月,而且闰年都出现在冬至(和大寒)月龄大于12/19的年份。文帝后元元年后,由于闰月分布有了改变,冬至不再固定在十一月了,反而大寒固定在十二月以及雨水固定在正月,而闰年则出现在雨水月龄大于12/19的年份。
表中虽然只列出几个节气,但我把所有二十四节气都计算了,发现在文帝后元元年前,除了冬至外没有其他二十四节气固定在一个月内,除了冬至和大寒外也没有其他节气月龄大于12/19的年份与闰年吻合。文帝后元元年后,除了大寒和雨水外,没有其他二十四节气固定在一个月内;除了雨水外,没有其他二十四节气月龄大于12/19的年份与闰年吻合。这些资料或许是研究这段期间置闰法则的重要线索。
备 注 和 参 考 文 献
[注一] 本文的主要目的是说明本网站对秦与汉初历法之复原法,并非学术论文,撰写时并无搜索所有的相关文献,如有文献遗漏,敬请原谅。
[注二] 至今我仍摸不透张培瑜07年文章表十的朔闰表是怎样算出的。只要知道其中一个合朔的日期和小余,其他合朔的日期和小余就可用张培瑜采用的朔策(29+663/1249)日计算出,但是表十只有日干支,没有给出小余。但这问题也不难解决,以表十的第一个合朔为例,合朔小余有1249个可能:0、1/1249、2/1249、……、1248/1249。从汉高祖元年十月到汉武帝元封六年后九月有1262个朔日,只要把这1249个可能的小余一一检验,就可知道哪个小余值可得出完全符合表十的1262个朔日干支(略去表十最后一行的太初元年朔日)。我编写了简单的计算机程式,得出这1249个可能的小余之中,只有611/1249能满足表十的1262个朔日干支。每月小余增加663,而mod(611+195×663, 1249) = 0,由此可知汉高祖元年十月后第195个合朔发生在夜半,但是这个朔是汉惠帝四年八月朔(公元前191年8月21日),日干支是丙戌,与文章所载的15蔀蔀首日名没有一个相符。根据采用的朔策,一蔀有1249×29+663=36884日,而36884×3=9221×12,所以蔀首日名地支以三蔀循环一周,如果戌是其中一地支,则其余蔀首日名地支只能是午和寅,但文章所列出的蔀首日名的三个可能地支是子、申和辰,显然与丙戌不相容。但是以汉惠帝四年八月丙戌合朔发生在夜半这假设确能得出符合表十的所有朔日干支。
如果假设表十的干支不完全正确,则可求出一个可能的结果。这假设是汉高祖元年十月的朔小余是613/1249,这样的话就有两个干支与表十不符:汉武帝建元四年五月朔和武帝元鼎四年十二月朔。有趣的是这两个不合的日干支反而符合李忠林12文章的朔闰表。由于mod(613+860×663, 1249) = 0,高祖元年十月朔后的第860个朔日发生在夜半,这朔恰巧就是武帝建元四年的五月朔,日干支由表十的癸卯改为甲辰,而甲辰是文章列出的蔀首日名其中之一。由于这不是四分术,蔀首只是合朔发生在夜半,但不保证气朔齐同。用蔀日36884往前推,看看是否可以找到一个以某一节气合朔夜半齐同的历元,使二十四节气的时刻接近颛顼历的二十四节气时刻。我发现一个可能的历元是前6297年庚申日夜半芒种合朔齐同(公历日期是前6297年6月12日,儒略日数是-578393.5),用此历元计算的节气时刻在公元前150年比颛顼历的约早10分钟。复原历法的岁实比四分术的岁实稍短,用此历元计算的节气时刻在汉初比颛顼历迟约15分钟, 在武帝太初元年时却比颛顼历早约30分钟。表十是不是用这个历元计算?那两个朔日干支是不是真的错了?[注三] 用李忠林文章所述的历元计算出汉高祖七年五月朔的日干是己卯,但是即使不用历元计算也可推出表中五月朔干支不对,而且应该是己卯。这可从汉高祖七年四月朔和六月朔的日干支看出。表中列出四月朔和六月朔的日干支都是己酉,由此可知四月朔与六月朔相差六十日,唯一的可能是四月和五月都是大月。所以五月朔干支是己酉之后第三十个干支,即己卯。
[注四] 《三千五百年历日天象》自汉武帝太初元年正月起采用新历法;从秦始皇三十一年(N-215)十月到太初元年十二月采用作者根据《元光元年历谱》复原的历法张培瑜78;从秦始皇二十六年(N-220)十月到秦始皇三十年(N-216)九月用颛顼历。《三千五百年历日天象》并没有说明这些细节,以上结论是比较书中历表和张培瑜的另一本书《中国先秦史历表》张培瑜87中的历表推断的。《三千五百年历日天象》载太初元年十二月和正月连续两月皆是小月,这在平朔法是不可能的,显然是正月改历的结果。
[注五] 实际合朔时刻用现代天文的计算方法,即这pdf文件所述的方法,但是岁差要用该文7.2节所说的Vondrák等人的岁差模型计算,算出的TDB时刻用该文第8节的方法转化为世界时UT1时刻。历法合朔时刻用上面公式(3)计算JD(Mi),这可视为是当地的地方时。秦朝京城咸阳和西汉京城长安的地理位置都很接近现在的陕西省西安市,经度大约是东经108.9°,所以京城地方时比UT1迟(108.9/15)小时=0.3025日,把JD(Mi)减去0.3025日便得历法合朔的UT1儒略日数,再减去实际合朔的UT1儒略日数便求得历法的后天日数。从秦王政元年十月朔到汉武帝太初元年四月朔总共有1764个合朔,图一就是用这1764个合朔的后天日数绘制而成。
[李忠林09] 李忠林,"试论秦汉初历法的置闰规则",《四川大学学报(哲学社会科学版)》,2009年第6期(总第165期),第5–11页。
[李忠林12] 李忠林,"秦至汉初(前246至前104)历法研究—以出土历简为中心",《中国史研究》,2012年第二期,第17–69页。
[李忠林16] 李忠林,《秦至汉初历法研究》,中华书局(北京),2016年1月。
[张培瑜78] 张培瑜, "汉初历法讨论",《中国天文学史文集》,科学出版社(北京),1978年四月,第82–94页。
[张培瑜87] 张培瑜,《中国先秦史历表》,齐鲁书社(济南),1987年6月。
[张培瑜97] 张培瑜,《三千五百年历日天象》,大象出版社,1997年7月。
[张培瑜07] 张培瑜, "根据新出历日简牍试论秦与汉初的历法",《中原文物》, 2007年第5期,第62–77页。
[张陈薄胡] 张培瑜、陈美东、薄树人和胡铁珠,《中国古代历法》,中国科学出版社(北京),2008年3月。